
 |
|||
| set | problems | soln |
| P-01 |
a. For the x-axis shifted boundary conditions presented in the differential equations handout, re-solve (2a) and obtain (7). Then substitute the redefined boundaries into (6) and verify that the solution is indeed shift independent. DO NOT USE MAPLE!!! b. Starting with (24) in the interpolation handout, complete the derivation of the cubic basis function (25). You may use Maple for this. c. For an element domain of (0,pi/2), interpolate Q(x)=cos(x) using linear, quadratic, and cubic basis functions. Clearly report the functional forms of Qe(x) for each approximation. Include a graph showing the original function and the three approximations. Comment on accuracy. |
soln |
| P-02 |
a. Per the two options for solving the global matrix statement presented in the assembly handout, employ option 1 and verify that the obtained nodal temperature solutions agree with (9) and that the boundary heat flux agrees with (11). You may use Maple. b. Starting with (1), repeat the assembly and solution process for a 3 element (4 node) uniform discretization of the domain (0,L). Include a plot of the exact solution and the M=2, M=3 finite element results (making sure the nodes are connected by linear functions!) for problem data specified in the text, page 32 problem 1. Comment on solution accuracy AND effort required. c. Determine the master matrices [A211L] and [A200L]. d. Apply the recipe steps 1 through 6 and obtain the GWSh for the following ODE and BC set 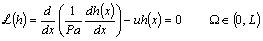 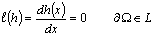  |
soln |
| P-03 |
a. From the higher order handout, verify equation (11), the derivative of {N3}. b. Verify equation (17), the element master matrix [A211C]. c. Verify equation (21), the element master matrix [A200C]. d. From the convergence handout, start with (1) and fill in the algebraic detail to obtain the quantitative error estimate (6) and error slope (7). |
soln |
| P-04 |
a. Integrate the element master matrix [A3011L] and verify the metric to be -1. b. From the Euler-Bernoulli beam handout, redo the integration-by-parts for I(x) and generate the syntactical form of the GWSh, hence introduce the [A3101k] master matrix. c. From the second Euler-Bernoulli beam handout, repeat the shear recovery analysis to obtain the slope distribution from the nodal solutions of deflection. |
soln |
| P-05 | a. From the Timeshenko beam handout, repeat the analysis for variable moment of inertia I(x) and cross-sectional area A(x). | soln |
| P-06 | a. From the non-linear heat conduction handout, derive the residual and jacobian for the given quadratic variation in thermal conductivity. | soln |
| P-07 |
a. For transient heat transfer with no source and Dirichlet boundary conditions from the transient heat conduction handout, apply GWS + ThetaTS, hence verify (10). Then apply Newton and verify the jacobian and residual terms in the attached code. b. For transient accuracy and convergence from the transient accuracy and convergence handout, obtain the theoretical error convergence rate for a mesh under uniform temporal refinement. Then derive the necessary temporal refinement so that the temporal error will decrease as fast as the spatial error for a linear basis under uniform refinement. |
soln |
| P-08 | soln | |
| P-09 | No problems | soln |
| TOP | ||
|
Prof. Zac Chambers Last modified: |