| Lab 03: AM and FM Sinusoidal Signals |
 The objective of this lab is to introduce more complicated
signals that are related to the basic sinusoid.
These are signals which implement frequency modulation (FM) and
amplitude modulation (AM) are widely used in communication systems
such as radio and television, but they also can be used to create
interesting sounds that mimic musical instruments.
The objective of this lab is to introduce more complicated
signals that are related to the basic sinusoid.
These are signals which implement frequency modulation (FM) and
amplitude modulation (AM) are widely used in communication systems
such as radio and television, but they also can be used to create
interesting sounds that mimic musical instruments.
|
| Lab 04: Music Synthesis - Synthesis of Sinusoidal Signals |
 In this lab, we will synthesize more complicated sinusoidal waveforms
composed of sums of sinusoidal signals, each with a different
frequency. The sounds synthesized will one of several songs.
[Files]
In this lab, we will synthesize more complicated sinusoidal waveforms
composed of sums of sinusoidal signals, each with a different
frequency. The sounds synthesized will one of several songs.
[Files]
|
| Lab 04a: Speech Synthesis - Synthesis of Sinusoidal Signals |
In this lab, we will synthesize more complicated sinusoidal waveforms
composed of sums of sinusoidal signals, each with a different
frequency. The sounds synthesized will sound like a voice.
[Files]
|
| Lab 04a: Speech Synthesis - Synthesis of Sinusoidal Signals |
In this lab, we will synthesize more complicated sinusoidal waveforms
composed of sums of sinusoidal signals, each with a different
frequency. The sounds synthesized will sound like a voice.
|
| Lab 05: FM Synthesis for Musical Instruments |
The objective of this lab is to introduce more complicated signals that
are related to the basic sinusoid.
These are signals which implement frequency modulation (FM) and
amplitude modulation (AM) are widely used in communication systems
such as radio and television), but they also can be used to create
interesting sounds that mimic musical instruments.
[Files]
|
| mp01: Jingle Bells Synthesizer |
In this lab, we will synthesize more complicated sinusoidal waveforms
composed of sums of sinusoidal signals, each with a different
frequency. The sounds synthesized will one of several songs.
|
| Lab 08: Frequency Response: Bandpass & Nulling Filters |
The goal of this lab is to study the response of FIR filters to
inputs such as complex exponentials and
sinusoids. In the experiments of this lab, you will use firfilt(),
or conv(), to implement filters and
freqz() to obtain the filter's frequency response. As a result,
you should learn how to characterize a
filter by knowing how it reacts to different frequency components in the input.
This lab also introduces two practical filters: bandpass filters
and nulling filters. Bandpass filters can be
used to detect and extract information from sinusoidal signals, e.g.,
tones in a touch-tone telephone dialer.
Nulling filters can be used to remove sinusoidal interference, e.g.,
jamming signals in a radar.
|
| Lab 09: Encoding and Decoding Touch-Tone Signals |
This lab introduces a practical application where sinusoidal
signals are used to transmit information: a touchtone
dialer. Bandpass FIR filters can be used to extract the
information encoded in the waveforms. The goal
of this lab is to design and implement bandpass FIR filters in MATLAB,
and do the decoding automatically.
In the experiments of this lab, you will use
firfilt(), or conv(),
to implement filters and freqz() to
obtain the filter's frequency response. As a result,
you should learn how to characterize a filter by knowing
how it reacts to different frequency components in the input.
[Files]
|
| Lab 10: Octave Band Filtering |
This lab introduces a practical application where we attempt
to extract information from sinusoidal signals -
in this case, piano notes. Bandpass FIR filters can be
used to extract the information encoded in the waveforms.
The goal of this lab is to design and implement several
bandpass FIR filters in MATLAB, and use the
filtered outputs to determine automatically which note is being played.
However, since there are 88 keys on
the piano, we will only require the system to figure
out which octave the note is in, not the exact note. In
the experiments of this lab, you will use
firfilt(), or conv(),
to implement filters and freqz() to
obtain the filter's frequency response. As a result,
you should learn how to characterize a filter by knowing
how it reacts to different frequency components in the input.
[Files]
|
| mp03: Tone Removal |
In this mini-project you will Write a simple MATLAB
program that removes unwanted tones from a wav file.
The file SunshineSquare.wav has had some unwanted tones added to it.
Your job is to remove the tones so you can hear the message better.
[Files]
|
| Lab 09: Encoding and Decoding Touch-Tone Signals |
This lab introduces a practical application where sinusoidal
signals are used to transmit information: a touchtone
dialer. Bandpass FIR filters can be used to extract the
information encoded in the waveforms. The goal
of this lab is to design and implement bandpass FIR filters in MATLAB,
and do the decoding automatically.
In the experiments of this lab, you will use
firfilt(), or conv(),
to implement filters and freqz() to
obtain the filter's frequency response. As a result,
you should learn how to characterize a filter by knowing
how it reacts to different frequency components in the input.
[Files]
|
| Lab 10: Octave Band Filtering |
This lab introduces a practical application where we attempt
to extract information from sinusoidal signals -
in this case, piano notes. Bandpass FIR filters can be
used to extract the information encoded in the waveforms.
The goal of this lab is to design and implement several
bandpass FIR filters in MATLAB, and use the
filtered outputs to determine automatically which note is being played.
However, since there are 88 keys on
the piano, we will only require the system to figure
out which octave the note is in, not the exact note. In
the experiments of this lab, you will use
firfilt(), or conv(),
to implement filters and freqz() to
obtain the filter's frequency response. As a result,
you should learn how to characterize a filter by knowing
how it reacts to different frequency components in the input.
[Files]
|
| Lab 11: PeZ - The z, n, and ω Domains |
The objective for this lab is to build an intuitive understanding of
the relationship between the location of poles and zeros in the
z-domain, the impulse response h[n] in the n-domain,
and the frequency
response H(ejω) (the ω-domain). A
graphical user interface (GUI) called
PeZ was written in MATLAB
for doing interactive explorations of the three domains.
|
| mp04 - PeZ |
In this mini-project you will experiment with PeZ to learn the connection
between pole-zero placement and frequency response. Given this information
you will redo the Tone Removal Mini-Project using an IIR.
|
| mp05: - Note Detection |
For this mini project you will write a simple function that
listens to a tone and identifies what note it is.
[Files]
|
| mp06: Simple Song Detection |
For this mini project you will write a simple function that
listens to a wav file of a simple song and identifies
the notes being played.
The wav files have some simple songs on which you can practice.
[Files]
|
| mp07: Swiss Army Knife |
You have gotten to the point in your studies that you can
understand DSP papers that appear in IEEE publications.
The purpose of this project is to read one such paper
and reproduce some of its results.
|
| Lab 17: Digital Communication: FSK Signals (Encoding) |
Perhaps an apt title for this quick introduction to
Frequency Shift Keying (FSK) Modems would be everything
you wanted to know about FSK Modems but were afraid to ask!
The goal of this lab (and the next one) is to understand a simple modem,
the Frequency Shift Keying
(FSK) Modem, referred to by the International Telecommunications Union
(I.T.U.) as V.21.
This lab presents how to construct the FSK encoder.
|
| Lab 18: Digital Communication: FSK Signals (Decoding) |
Perhaps an apt title for this quick introduction to
Frequency Shift Keying (FSK) Modems would be everything
you wanted to know about FSK Modems but were afraid to ask!
The goal of this lab (and the previous one) is to understand a simple modem,
the Frequency Shift Keying
(FSK) Modem, referred to by the International Telecommunications Union
(I.T.U.) as V.21.
This lab presents how to decode FSK signals.
[Files]
|
| Lab 19: The Fast Fourier Transform |
The goal of this lab is to introduce the Fast Fourier Transform (FFT) for efficient
computer calculation of the Fourier Transform and then to investigate some of the
Fourier Tranform's properties.
|
| Lab 20: Extracting Frequencies of Musical Tones |
 This lab is built around a single project that involves the implementation
of a system for automatically writing a musical score by analyzing the
frequency content of a recording (a sampled signal).
A primary component of such a system is the spectrogram which produces a
time-frequency representation of the recorded waveform.
However, to make a working system, several other processing components are
needed after the spectrogram to extract the important information related
to the notes.
The design of these additional blocks will lead naturally to a deeper
understanding of what the spectrogram actually represents.
[Files]
This lab is built around a single project that involves the implementation
of a system for automatically writing a musical score by analyzing the
frequency content of a recording (a sampled signal).
A primary component of such a system is the spectrogram which produces a
time-frequency representation of the recorded waveform.
However, to make a working system, several other processing components are
needed after the spectrogram to extract the important information related
to the notes.
The design of these additional blocks will lead naturally to a deeper
understanding of what the spectrogram actually represents.
[Files]
|


 1. Introduction
1. Introduction
 2. Sinusoids
2. Sinusoids
 In this lab we introduce the fundamentals of Matlab. Matlab is
a programming environment that you will find helpful for many of
the exercises in this text.
In this lab we introduce the fundamentals of Matlab. Matlab is
a programming environment that you will find helpful for many of
the exercises in this text.
 Manipulating sinusoid functions using complex exponentials turns
trigonometric problems into simple arithmetic and algebra.
In this lab, we first review the complex exponential signal and the
phasor addition property needed for adding cosine waves.
Then we will use Matlab to make plots of phasor diagrams that show
the vector addition needed when combining sinusoids.
[Files]
Manipulating sinusoid functions using complex exponentials turns
trigonometric problems into simple arithmetic and algebra.
In this lab, we first review the complex exponential signal and the
phasor addition property needed for adding cosine waves.
Then we will use Matlab to make plots of phasor diagrams that show
the vector addition needed when combining sinusoids.
[Files]
 3. Spectrum Representation
3. Spectrum Representation
 The objective of this lab is to introduce more complicated
signals that are related to the basic sinusoid.
These are signals which implement frequency modulation (FM) and
amplitude modulation (AM) are widely used in communication systems
such as radio and television, but they also can be used to create
interesting sounds that mimic musical instruments.
The objective of this lab is to introduce more complicated
signals that are related to the basic sinusoid.
These are signals which implement frequency modulation (FM) and
amplitude modulation (AM) are widely used in communication systems
such as radio and television, but they also can be used to create
interesting sounds that mimic musical instruments.
 In this lab, we will synthesize more complicated sinusoidal waveforms
composed of sums of sinusoidal signals, each with a different
frequency. The sounds synthesized will one of several songs.
[Files]
In this lab, we will synthesize more complicated sinusoidal waveforms
composed of sums of sinusoidal signals, each with a different
frequency. The sounds synthesized will one of several songs.
[Files]
 4. Sampling and Aliasing
4. Sampling and Aliasing
 5. FIR Filters
5. FIR Filters
 The goal of this lab is to learn how to implement FIR filters
in MATLAB, and then study the response of FIR
filters to various signals, including images and speech.
As a result, you should learn how filters can create
interesting effects such as blurring and echoes. In addition,
we will use FIR filters to study the convolution
operation and properties such as linearity and time-invariance.
[Files]
The goal of this lab is to learn how to implement FIR filters
in MATLAB, and then study the response of FIR
filters to various signals, including images and speech.
As a result, you should learn how filters can create
interesting effects such as blurring and echoes. In addition,
we will use FIR filters to study the convolution
operation and properties such as linearity and time-invariance.
[Files]
 6. Frequency Response of FIR Filters
6. Frequency Response of FIR Filters
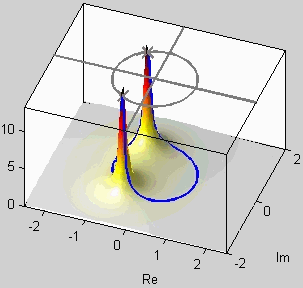 7. Z-Transform
7. Z-Transform
 8. IIR Filters
8. IIR Filters
 9. Continuous-Time Signals and LTI Systems
9. Continuous-Time Signals and LTI Systems
 10. Frequency Response
10. Frequency Response
 11. Continuous-Time Fourier Transform
11. Continuous-Time Fourier Transform
 12. Filtering, Modulation, and Sampling
12. Filtering, Modulation, and Sampling
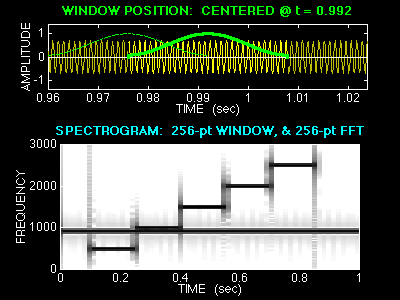 13. Computing the Spectrum
13. Computing the Spectrum
 This lab is built around a single project that involves the implementation
of a system for automatically writing a musical score by analyzing the
frequency content of a recording (a sampled signal).
A primary component of such a system is the spectrogram which produces a
time-frequency representation of the recorded waveform.
However, to make a working system, several other processing components are
needed after the spectrogram to extract the important information related
to the notes.
The design of these additional blocks will lead naturally to a deeper
understanding of what the spectrogram actually represents.
[Files]
This lab is built around a single project that involves the implementation
of a system for automatically writing a musical score by analyzing the
frequency content of a recording (a sampled signal).
A primary component of such a system is the spectrogram which produces a
time-frequency representation of the recorded waveform.
However, to make a working system, several other processing components are
needed after the spectrogram to extract the important information related
to the notes.
The design of these additional blocks will lead naturally to a deeper
understanding of what the spectrogram actually represents.
[Files]
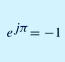 A. Complex Numbers
A. Complex Numbers