2. Sinusoids

Overview: In chapter two, the most basic waveform in signal processing, the cosine wave, is presented. The mathematical formula for the cosine wave, in its most general form is given below:

x(t)=A cos(2πf₀t+φ)

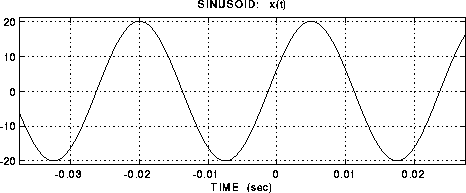
Where x(t) is a function of the time variable t. The amplitude of the cosine is given by the real number A. The frequency of the of the cosine wave is f₀, and in the audio experiments that follow, it is the frequency that determines what we hear. Finally, the phase of the sinusoid is given by the parameter φ. A plot of a cosine is given in the figure below:

Also in chapter two, the phasor representation of sinusoids is presented. A new signal is introduced called the complex exponential:

x(t)=A e^{j(2πf₀t+φ)}

The generalization to complex exponentials is important for later work in Fourier analysis, so we are laying a foundation for the future. The real part of the complex exponential is a cosine, and its imaginary part is the sine function, so a plot of the complex exponential is a rotating vector with a constant length A. This signal is called a rotating phasor.

Homework

Labs - MATLAB

Lab 01: Introduction to Matlab	In this lab we introduce the fundamentals of Matlab. Matlab is a programming environment that you will find helpful for many of the exercises in this text.
Lab 02a: Introduction to Complex Exponentials - Multipath	Manipulating sinusoid functions using complex exponentials turns trigonometric problems into simple arithmetic and algebra. In this lab, we first review the complex exponential signal and the phasor addition property needed for adding cosine waves. Then we will use Matlab to make plots of phasor diagrams that show the vector addition needed when combining sinusoids. [Files]
Lab 02b: Introduction to Complex Exponentials - Direction Finding	Manipulating sinusoid functions using complex exponentials turns trigonometric problems into simple arithmetic and algebra. In this lab, we first review the complex exponential signal and the phasor addition property needed for adding cosine waves. Then we will use Matlab to make plots of phasor diagrams that show the vector addition needed when combining sinusoids. [Files]

Demos

	Rotating Phasor	p21 - Shows how the real part of the rotating phasors traces out a sinusoid versus time.
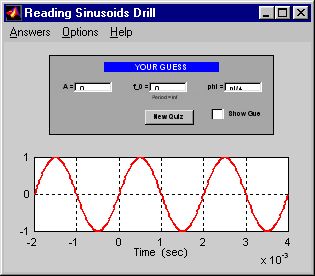	Sine Drill	p12 - Tests the users ability to determine basic parameters of a sinusoid.
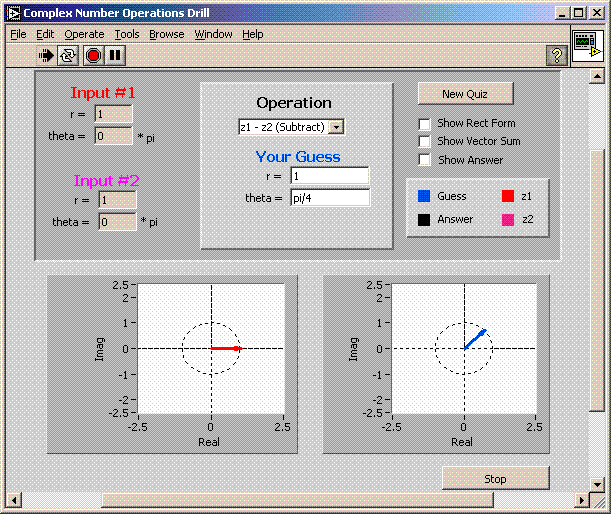	ZDrill	p26 - Tests users ability to calculate the result of simple operations on complex numbers. The program emphasizes the vectorial view of a complex number. The following six operations are supported: Add Subtract Multiply Divide Inverse Conjugate