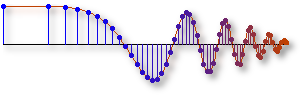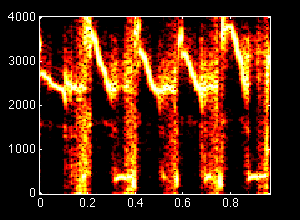
3. Spectrum Representation
Overview: In chapter three, the graphical representation of signals
via their frequency content is treated. We have spent a lot of time
learning about the properties of sinusoidal waveforms of the form:
)
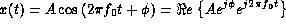
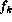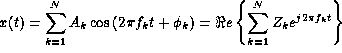
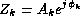is the complex phasor amplitude.
Homework
Labs - MATLAB
| Lab 03: AM and FM Sinusoidal Signals |
The objective of this lab is to introduce more complicated
signals that are related to the basic sinusoid.
These are signals which implement frequency modulation (FM) and
amplitude modulation (AM) are widely used in communication systems
such as radio and television, but they also can be used to create
interesting sounds that mimic musical instruments.
|
| Lab 04: Music Synthesis - Synthesis of Sinusoidal Signals |
In this lab, we will synthesize more complicated sinusoidal waveforms
composed of sums of sinusoidal signals, each with a different
frequency. The sounds synthesized will one of several songs.
[Files]
|
| Lab 04a: Speech Synthesis - Synthesis of Sinusoidal Signals | In this lab, we will synthesize more complicated sinusoidal waveforms composed of sums of sinusoidal signals, each with a different frequency. The sounds synthesized will sound like a voice. [Files] |
| Lab 04a: Speech Synthesis - Synthesis of Sinusoidal Signals | In this lab, we will synthesize more complicated sinusoidal waveforms composed of sums of sinusoidal signals, each with a different frequency. The sounds synthesized will sound like a voice. |
| Lab 05: FM Synthesis for Musical Instruments | The objective of this lab is to introduce more complicated signals that are related to the basic sinusoid. These are signals which implement frequency modulation (FM) and amplitude modulation (AM) are widely used in communication systems such as radio and television), but they also can be used to create interesting sounds that mimic musical instruments. [Files] |
| mp01: Jingle Bells Synthesizer | In this lab, we will synthesize more complicated sinusoidal waveforms composed of sums of sinusoidal signals, each with a different frequency. The sounds synthesized will one of several songs. |
Demos
 |
3-3,4,5,6 Beat Note | p41,42 - Shows the effect of multiplying two sinusoids that are close in frequency. |
 |
FM Synthesis |
p63 - This demo gives the mathematical derivation of how instrument sounds can be
synthesized using the principles of frequency modulation.
The example sounds include a bell and a clarinet.
|
|
3-14,17,19,20 Fourier Series Demo | p52,54,56,57 - Shows how any periodic signal can be approximated as a sum of sinusoids. It allows you to choose from several input signals and creates an approximati on to the signal you choose. You can select how mnay cosine terms to use in the approximation. |
