7. Z-Transform

Overview: In chapter 7 the
z-Transform is introduced. This
algebraic method introduces polynomials into the analysis of linear systems.
Thus the well-known operations of factoring of polynomials, multiplying and
dividing polynomials have powerful consequences and interpretations for
digital filters. In general, the
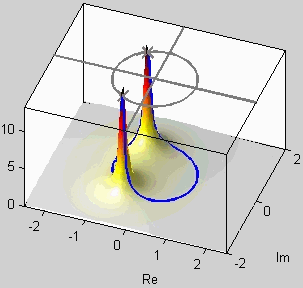
z-Transform system functions are
rational functions-the ratio being a numerator polynomial divided by a
denominator polynomial. Of particular interest are the polynomial roots
which, in the case of feedback filters, make up the
poles and
zeros of the filter. In the long run, most properties of digital
filters can be restated in terms of the pole and zero locations in the
complex
z-plane. For example, stability of a filter requires that
the poles lie inside the unit circle.
| Lab 09: Encoding and Decoding Touch-Tone Signals |
This lab introduces a practical application where sinusoidal
signals are used to transmit information: a touchtone
dialer. Bandpass FIR filters can be used to extract the
information encoded in the waveforms. The goal
of this lab is to design and implement bandpass FIR filters in MATLAB,
and do the decoding automatically.
In the experiments of this lab, you will use
firfilt(), or conv(),
to implement filters and freqz() to
obtain the filter's frequency response. As a result,
you should learn how to characterize a filter by knowing
how it reacts to different frequency components in the input.
[Files]
|
| Lab 10: Octave Band Filtering |
This lab introduces a practical application where we attempt
to extract information from sinusoidal signals -
in this case, piano notes. Bandpass FIR filters can be
used to extract the information encoded in the waveforms.
The goal of this lab is to design and implement several
bandpass FIR filters in MATLAB, and use the
filtered outputs to determine automatically which note is being played.
However, since there are 88 keys on
the piano, we will only require the system to figure
out which octave the note is in, not the exact note. In
the experiments of this lab, you will use
firfilt(), or conv(),
to implement filters and freqz() to
obtain the filter's frequency response. As a result,
you should learn how to characterize a filter by knowing
how it reacts to different frequency components in the input.
[Files]
|