A. Complex Numbers
Overview: In Appendix A, the basic manipulations of complex numbers
are presented. The algebraic rules for combining
complex numbers are reviewed, and then a geometric viewpoint is
taken to explain various operations by drawing vector diagrams. The
following four significant ideas will be pointed out concerning
complex numbers:
- Simple Algebraic Rules: operations on complex numbers
(z=x+jy) follow exactly the
same rules as real numbers, with
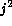replaced everywhere
by -1. - Eliminate Trigonometry: in polar form,
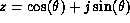appears in formulas,
so many trig identities reduce to simple algebraic operations on a
complex number. - Represent Vectors: a vector drawn from the origin to a point
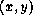in a two-dimensional plane
is equivalent to z=x+jy. The algebraic rules
for z are, in effect, the basic rules for vector operations. More
important, however, is the visualization gained from the vector
diagrams. - Represent Sinusoids: the magnitude and phase of the sinusoid are used to define the polar form of a complex number. Then operations such as adding sine waves are reduced to adding complex numbers.
