Given the relations between the front and back, we can now create
an initial back-tire track segment. Recall from the description
of our construction process, once we have an initial back-tire
track segment, it is easy to construct an initial front-tire track
segment using the relation
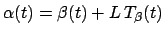 .
The construction of our initial back-tire track segment follows
from an interpolation scheme using conditions that can be derived
from the geometry of bicycle tracks and the defining property of
ambiguous tracks.
.
The construction of our initial back-tire track segment follows
from an interpolation scheme using conditions that can be derived
from the geometry of bicycle tracks and the defining property of
ambiguous tracks.
We derive the necessary and sufficient conditions on the back-tire
track, by examining the relations that follow from the defining
property of ambiguous bicycle tracks. Recall, the defining
property of ambiguous bicycle tracks is that the front-tire track
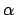 can be described as either
can be described as either
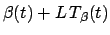 or
or
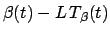 in terms of the back-tire track
in terms of the back-tire track 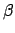 .
This implies that for each
.
This implies that for each 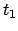 there is a
there is a 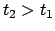 such that
such that
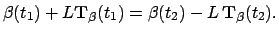 |
(9) |
This then implies that the geometry (Frenet frames and curvatures)
of the front-tire track can be computed from either description
and we must obtain the same values at the corresponding 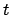 -values
-values
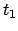 and
and 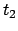 . Therefore, we must have
and
. Therefore, we must have
and
These properties will form the conditions that we need in order to generate
a pair of ambiguous tire tracks. It is possible to derive additional
smoothness conditions by differentiating the curvature of the front-tire
track with respect to arc-length, but these are not needed in our method.
From these conditions, we can easily construct an initial back-tire
track segment ![$ \beta:[0,1]\to \mathbb{R}^2$](images1/img87.gif) which will be thrice differentiable. We
first choose an isosceles triangle
which will be thrice differentiable. We
first choose an isosceles triangle 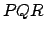 with
with 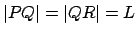 . Then, we set
. Then, we set 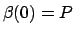 ,
, 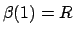 , and
, and
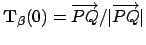 and
and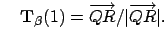 |
This ensures that
Next, we choose a tangent vector 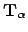 for the front-tire track at
for the front-tire track at 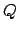 and a curvature
and a curvature 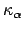 at
at 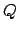 . These are used to define the curvature of the
. These are used to define the curvature of the 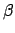 at
at 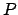 and
and 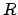 , and the derivative of the curvature
, and the derivative of the curvature 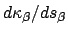 at
at 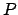 and
and 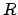 . The curvature
. The curvature 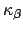 at
at 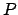 and
and 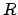 are given respectively by
are given respectively by
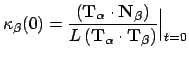
and
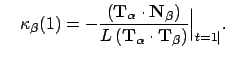 |
The derivative
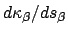 of the curvature with
respect to arc-length at
of the curvature with
respect to arc-length at 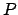 and
and 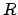 are then given by solving
and
for
are then given by solving
and
for
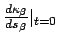 and
and
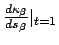 .
.
It is now a standard exercise in interpolation to create a curve ![$ \beta:[0,1]\to \mathbb{R}^2$](images1/img87.gif) that has these properties; prescribed values
for
that has these properties; prescribed values
for 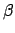 ,
, 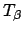 ,
, 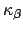 and
and 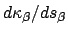 when
when 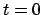 and
and 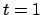 .
.
![\begin{equation*}\begin{aligned}&\left[\frac{1}{\sqrt{1 + (L\kappa_\beta)^2}} \...
...a)^2}} \mathbf{ N}_\beta \right]\Big\vert _{t=t_2} \end{aligned}\end{equation*}](images1/img85.gif)
![\begin{equation*}\begin{aligned}&\left[\frac{L\frac{d\kappa_\beta}{ds_\beta}}{(\...
...t{1 + (L\kappa_\beta)^2}}\right]\Big\vert _{t=t_2}. \end{aligned}\end{equation*}](images1/img86.gif)
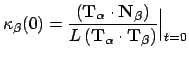
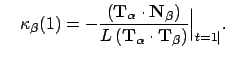
![$\displaystyle \kappa_{\alpha} = \left[L\frac{d\kappa_\beta}{ds_\beta} (\mathbf{...
...\frac{(\mathbf{ T}_\alpha \cdot \mathbf{ N}_\beta)}{L}\right] \Big\vert _{t=0}$](images1/img101.gif)
![$\displaystyle \kappa_{\alpha} = \left[L\frac{d\kappa_\beta}{ds_\beta} (\mathbf{...
...\frac{(\mathbf{ T}_\alpha \cdot \mathbf{ N}_\beta)}{L}\right] \Big\vert _{t=1}$](images1/img102.gif)