MODELLING THE SHAPE OF A COOKIE
an Undergraduate Research Project,
funded by National Science Foundation REU grants
DMS-0352940, DMS-0647121 |
|
Rose-Hulman Math REU page |
|
Participants |
Results |
Preprints |
| When baking a drop sugar cookie, one starts with a drop of cookie dough on
the cookie sheet. As the dough gets heated, it becomes a liquid and starts to achieves its equilibrium
shape. Then as it bakes it solidifies to its final equilibrium shape. See pictures below. |
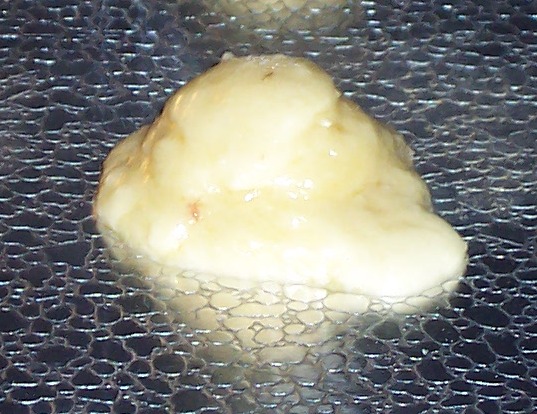
Drop of Cookie Dough
(becoming a liquid) |

Cookie Baking
(attaining shape) |

Baked Cookie
(cooling to final shape) |
PROBLEM:
Once the cookie is baked, can one recover the shape of the cookie knowing
only its wetted surface (the region that it is in contact with the cookie sheet), and properties
of the cookie dough (density, stiffness) and the size (volume) of the cookie? |
MATHEMATICAL MODEL:
The solution of this problem requires development of a mathematical model
governing the shape of a cookie. A simple heurestic model
is that the shape is given as an equilibrium capillary surface or a non-symmetric sessile drop. This
is the same physical phenomena that governs the shape of a water drop on a horizontal surface. The
justification for this model is that the shape of the cookie is obtained while the cookie is a liquid
in the baking process while it is first heated as the physical/chemical process of baking occurs.
In geometric terms, the model requires finding a surface with prescribed mean curvature. Analytically
this is determined by seeking a solution to a nonlinear elliptic partial differential equation which represents the
mean curvature or seeking a minimizer to the energy functional rof the cookie dough.
Given a surface described vectorially as
X(u,v) = x(u,v) i +
y(u,v) j + z(u,v) k
and parameters κ and λ
describing respectively the density and stiffness of the cookie dough and the size of the cookie, we
thus seek a surface with
H = κ z - λ,
where H is the mean curvature of the surface. In addition, we want the surface to meet the plane
z = 0 in a specified curve which we represent as the boundary of the region Ω.
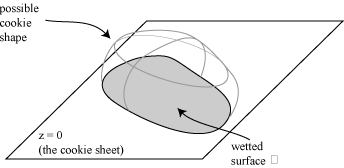
|
Questions to consider:
- How does the shape change depend on the physical parameters of the cookie κ and λ?
For instance, fixing the wetted surface Ω, is the location of the maximum value of the height of cookie
above the cookie sheet independent of κ and λ? If not, how does it vary? Moreover, can the
location of the maximum value of the height of the cookie above the cookie sheet be
predicted from the wetted surface Ω?
- How does the shape depend on the wetted surface Ω?
- When baking cookies, sometimes two cookies run together forming a double bubble cookie with
wetted surface as below. The cookie shape is then not smooth. What is the angle of intersection of the two
cookie bubbles? What does it depend on?
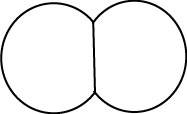 
- How does cooling affect shape?
- How does this model reflect the actual shape of a cookie?
- How can the model more accurately reflect the shape of a cookie?
|