(1) | Table of Contents |
Crummett and Western, Physics: Models and Applications,
Sections 25-1, 27-5
Halliday and Resnick, Fundamentals of Physics (5th ed.),
Sections 26-2, 28-6
Tipler, Physics for Scientists and Engineers (3rd ed.), Sections
21-1, 23-2
Consider a circuit such as that in Figure 1, in which a potential difference is applied to the series combination of a resistor and a capacitor. During any interval in which a constant potential difference is applied to the RC combination, the capacitor charges or discharges exponentially and the current to the capacitor has the form
(1)
The quantity RC is called the time constant of the RC combination. It has the dimensions of a time; in effect, it is an estimate of the time required to make a change in the potential differences in the circuit. From (1), the graph of the logarithm of the current vs. time will be linear, with slope -1/RC.
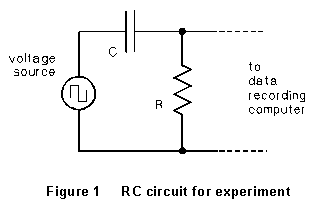In the experiment:
the voltage source in the experiment is a 10 Hz square wave generator,
providing a constant voltage for 50 ms in each half-cycle. For each corresponding
50-ms interval, the current in the circuit, and accordingly the voltage
across the resistance, will depend on time according to (1). You will use
this property to determine the capacitance of a large parallel-plate capacitor,
and also that of a small cylindrical capacitor.
(1) Use the digital voltmeter to measure the value of each resistor at your station. Be sure to use a scale which permits at least three significant figures. Use a meter stick to measure the dimensions of your 'large' capacitor. Note that paper clips serve as contacts to these large capacitors. Try not to disturb the paper clips, or tear the aluminum foil.
(2) Start the program ANALOGN.EXE in the C:\LAB directory. Go to the Preferences menu, then to the Analog Parameters menu. Set up for Channel A, -10v to +10v range, BURST mode. Set the burst mode parameters for 1000 data points, and 5000 Hz acquisition frequency. The Burst frequency adjustment must be zero.
(3) Preliminary waveform measurements: Make sure the clip lead connector is plugged into the blue box at one end, and the clip leads are not connected to anything, just lying there on the benchtop. Take some data, and look at the graph of voltage vs. time. Is it zero? Is it something else? Try to interpret your results.
Repeat the above with one of the lab partners contacting the metal part of the red clip lead. Record the graph features in your lab book. Try once again with a partner contacting the red lead with one hand and the black lead with the other. Discuss these results very briefly in the lab notebook.
(4) Now measure the capacitance of the large parallel-plane capacitor. Make sure that a set of clip leads is attached to channel A of the blue I/O Box (which connects to the computer). Set the function generator frequency as low as it will go (10 Hz), and make sure that a set of leads is connected to the rear of the Philips function generator where it says "TTL Output." Connect the resistor to one side of the capacitor, using the paper-clip connector. Connect the red lead from the Philips to the other side of the capacitor. Put the black Philips lead on the side of the resistor not connected to the capacitor. (You should now have the circuit of Figure 1.) Now put the clip leads from the computer across the resistor, with the black lead connected at the same place where the black Philips lead is placed.
Take a set of data. You should see a low, wavy line, with a few spikes in it, some going up, and some going down. Your clip leads are set up across the resistor, so you are looking at the potential difference across the resistor, which is proportional (V=IR) to the current through this resistor. A big voltage spike represents a lot of current through the resistor. In charging or discharging, the current through the resistor is proportional to exp(-t/RC). So if you examine the natural log of the voltage vs time, it should be a straight line of slope -1/RC. (There is some extraneous pickup which causes the wavy line, and means that the line is not perfectly straight.)
(5) Strike 'E' or 'e' for Edit. Edit lets you (by pressing F2) look at the ln of the voltage (It actually plots the ln of the absolute value of the voltage. For any voltage of zero, it pretends that the ln is zero.) Edit down to one of the spikes and look at ln(V). Use a line fit to determine the slope for that part of the line which is extremely straight. Record the equation of the line when you are satisfied that is is straight. If a line is not straight, look at another. It is easy to retake data, and you may want to look at several spikes before you like the straightness. Remember that not all of the line will be completely straight, due to the noise you saw with the clip leads open. Obtain three values of the slope. Use the average of these, and the resistor value, to calculate the capacitance. There is one capacitance meter in the lab. Get a capacitance reading from this meter. Compare your capacitance values to the capacitance from the formula
(2)
(
0 = 8.85 x
10-12 F/m) Do this before going on to the next part. The capacitance
formula (2) is for vacuum between the plates; it will be increased by a
factor of K with a dielectric present. What value of K is implied by your
results?
(6) Set up two capacitors in parallel with a group which has completed its work on a large capacitor. Determine the parallel value of capacitance, exactly as was done above. Record the data of both groups in your lab notebook. One group should do a trial, and the other group should do a trial.
(7) Small cylindrical capacitor measurement. There are a number of small cylindrical capacitors available, with resistors already soldered to them. These capacitors have a value around 0.01 µF microfarads. Determine the value of this capacitor just as you did for the large parallel-plate capacitor. Use both the RC slope method, and the capacitance meter. In the process, you must measure the resistance R with a meter.
The analysis you have done along the way needs to be collected and displayed. The average and standard deviation of three trials should be computed for each separate capacitance. It should be made clear how the measurements and results are connected. Compare theory and experiment wherever possible. Make sure overall results are displayed in a well-organized and clearly readable table.
from IFYCSEM -- 6/96 - last rev 7.97