| Table of Contents |
The most general case of error propagation is that in which the derived quantity q depends on several independent variables x, y, . . . The formula describing this case is kind of ugly, but it's easy to see how it comes about. First we recognize that Equation (7) still describes the error in q that would be produced by any one variable (say, x) alone. Call this sq|x. Then by Equation (7)
![]()
The notation q/x stands for the partial derivative of q(x, y, . . .) with respect to x. That just means you take the derivative with respect to x, while treating all the other variables as if they were constant.
The overall sq is just some combination of the contributions (sq|x, sq|y, . . .) from all the different variables that determine q. The question is, just how do they combine? One's first impulse is simply to add them:
![]() (THIS IS WRONG!!)
(THIS IS WRONG!!)
(Yes, we know that's what you've been taught to do in other courses. It's still wrong. Don't do it any more. Under any circumstances.) What's wrong with it is that the x, y, . . . are independent variables; just adding the uncertainties will overestimate the overall error, because it neglects the possibility that random error contributions due to different variables are just as likely to cancel as to add. It turns out (I'm not going to try to prove it to you) that the proper way to combine error contributions due to different independent variables is as the square root of the sum of squares:
![]()
The general rule for propagation of errors is therefore
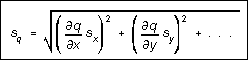 (9)
(9)
Example: Suppose that you've measured the time (t) required for an object to fall freely through a measured distance (y), and calculate the acceleration due to gravity from the formula g = 2y/t2. Your measured values are
y = 24.8 ± 0.4 cm and t = 0.224 ± 0.004 sec
so ![]()
Here ![]()
and ![]()
(Note that signs can be ignored, because the derivatives come into (9) only as the squares.) Thus (9) becomes
![]()
![]()
and our final result is ![]()
(It's usually good practice, when all the smoke has cleared, to round everything off to the point where the error has just one -- certainly never more than two -- significant figure appearing. Another point of good practice is never to round error limits significantly downward.)
Once again, there are a couple of special cases that you'll use over and over. All of these follow directly from Equation (9), and the ideas in the discussion that led up to it.
(1) Sum or Difference
for q = x + y or x - y, ![]() (10)
(10)
Using (8a), we can generalize this to the case of any linear sum. If A, B, etc., are constants, then
![]() (11)
(11)
Example: You've measured x = 12.57 ± 0.14 cm and y = 5.98 ± 0.09 cm in some experiment, and the result you want to calculate is q = x - 2y = 0.61 cm.
This is the case of Equation (11) with A = 1, B = -2:
![]() so
so ![]()
Notice in this example the relatively large uncertainty that results from taking the (small) difference of two numbers of comparable size.
(2) Product or Quotient
For q = xy or x/y 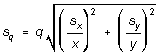
that is, ![]() (12)
(12)
where, as before, fx = sx/x , etc. Notice how this works; for a product or quotient, the fractional errors combine just as the absolute errors do for a sum or difference. Using (8b), we can generalize this to the general case of a product of powers. If A and the exponents m, n», etc., are constants, then
![]() (13)
(13)
Example: The calculation of g from measurements of time and distance, done above, has this form. We have g = y+1 t-2, so y and t take the place of x and y, m = +1, and n = -2. The measured values are
y = 24.8 ± 0.4 cm fy = 0.016 cm
t = 0.224 ± 0.004 sec ft = 0.018 sec
which gave g = 988.5 cm/s2
so ![]()
and ![]()
![]()
as we had before. Notice that in this case it's easier to have the "rule" to apply than it is to work the partial derivatives out numerically.
 (3) Rectangular
to Polar Conversion
(3) Rectangular
to Polar Conversion
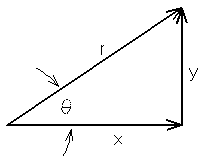
Suppose you've measured the components of a vector (see the sketch at right) and want its magnitude and direction. The formulas you need are
![]()
and 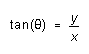
(Notice that must be in radians.) Thus
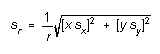
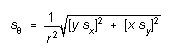 (14)
(14)
Example: You know the location of some landmark on a trip as 40 miles north and 26 miles east of your starting point, each within a standard error of 0.5 miles. You want to calculate its distance and "bearing". Then
![]()
![]()
thus ![]()
![]()
giving r = 47.7 ± 0.5 mi for the distance, and
= 0.994 ± 0.011 (radians) = 57.0 ± 0.6 for the bearing.
These are a few of the cases that you're most likely to run into in an elementary physics lab experiment. If you have to deal with more complicated examples, remember that you can apply Equation (9) in stages: combine two of your variables into a third, figure its error, combine it with one or more others, and so on. Sometimes this lets you use the special-case rules like (8) or (10) or (13), whereas applying (9) all at once might be a horrible mess.
We can use Equation (9) to get the formula given earlier for the standard deviation of the mean. The mean of N trials can be written
![]()
where x1, x2, . . . are the various trials of the same measurement x. Clearly
![]()
for every xi; and the standard deviation associated with each trial of x is just sx, calculated in the usual way. Therefore
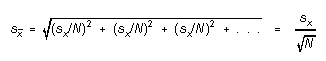
which is just Equation (3).
In any case, (9) is quite general, provided only that you have standard deviation estimates sx, sy, . . . for all the variables that your result depends on. Let me stress that it doesn't matter how the individual estimates were arrived at: from repeated trials of an experiment, from the manufacturer's specifications for an instrument, or just from your educated guess as to how closely you can read a meter stick.
Also, notice something else that you can learn from the structure of Equation (9). Each of the individual terms that are being combined is the contribution of one of the variables to the standard error of the result. (At one point I called it sq|x.) In practice, it often happens that one of these terms is much bigger than the others. If this is the case, it tells you a couple of things: first, that just figuring that one term - using Equation (7) instead of the messier (9) - will do, at least as a quick approximation; and second, that if you want to improve the experiment, which of your measurements you need to work on.