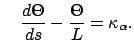To describe our method for extending the back-tire track, let ![$ \beta:[0,1]\to \mathbb{R}^2$](images1/img87.gif) be an initial back-tire track segment constructed
by one of the methods in the previous section, and let
be an initial back-tire track segment constructed
by one of the methods in the previous section, and let ![$ \alpha:[0,1] \to \mathbb{R}^2$](images1/img151.gif) be the front-tire track obtained by pushing
the bicycle in both possible directions on the back tire track, that
is
be the front-tire track obtained by pushing
the bicycle in both possible directions on the back tire track, that
is
The construction methods for  in the previous section ensure that
in the previous section ensure that  described above is twice differentiable with respect to arclength.
In this section, we use the differential equations describing the geometry
of bicycle tracks to extend the back-tire track
described above is twice differentiable with respect to arclength.
In this section, we use the differential equations describing the geometry
of bicycle tracks to extend the back-tire track  to
to 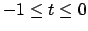 . We will only describe the method for extending the
back-tire track to
. We will only describe the method for extending the
back-tire track to 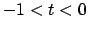 , as once we have the new back-tire track we can repeat this procedure
to extend the track in an iterative manner to
, as once we have the new back-tire track we can repeat this procedure
to extend the track in an iterative manner to 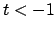 . The extension for
. The extension for 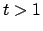 is then established by applying the same method to the initial
back-tire track
is then established by applying the same method to the initial
back-tire track 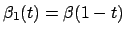 that has the opposite orientation as
that has the opposite orientation as 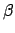 .
.
Let 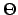 be the turning angle between
be the turning angle between 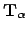 and
and 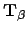 . This is defined for
. This is defined for 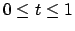 . Our construction method is based upon extending
. Our construction method is based upon extending 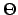 to
to 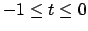 , and then using
, and then using 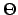 to define the curvature of the back-tire track for
to define the curvature of the back-tire track for 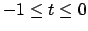 , and the fundamental theorem of plane curves to extend
the back-tire track. The turning angle
, and the fundamental theorem of plane curves to extend
the back-tire track. The turning angle 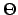 is extending by solving the differential equation
is extending by solving the differential equation
using the definition of 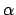 above to compute the curvature
above to compute the curvature 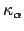 for
for 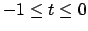 . The existence of a solution follows from the existence
and uniqueness of solutions to differential equations at least for a
short time
. The existence of a solution follows from the existence
and uniqueness of solutions to differential equations at least for a
short time 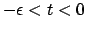 . However, it is not hard using comparison theorems
to show that there is a solution for
. However, it is not hard using comparison theorems
to show that there is a solution for 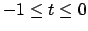 . But, it is not possible to show that a generic solution
must satisfy
. But, it is not possible to show that a generic solution
must satisfy 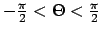 . In fact, one can easily
construct examples of initial segments for which the solution fails
to satisfy
. In fact, one can easily
construct examples of initial segments for which the solution fails
to satisfy 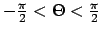 .
.
Rather than give a formal study of the existence of solutions satisfying
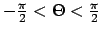 , we supply a informal
perturbation argument that one can extend some initial segments practically
indefinitely. We first note that if
, we supply a informal
perturbation argument that one can extend some initial segments practically
indefinitely. We first note that if 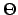 is identically a constant on
is identically a constant on 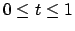 , then
, then 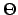 extends to a constant for
extends to a constant for 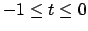 . Thus, an initial segment of constant
. Thus, an initial segment of constant 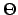 (an arc of a circle or a line segment) will generate a circle
or a straight line (curves of constant curvature). If we start with
a small perturbation of a segment of constant curvature, then it seems
reasonable that with a small enough perturbation one can extend the
track practically indefinitely. Of course, we will not specify what
we mean by small.
(an arc of a circle or a line segment) will generate a circle
or a straight line (curves of constant curvature). If we start with
a small perturbation of a segment of constant curvature, then it seems
reasonable that with a small enough perturbation one can extend the
track practically indefinitely. Of course, we will not specify what
we mean by small.
Our argument relies on the use of comparison theorems to show the
existence of a solution 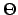 for
for 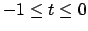 , and the continuous dependence of the solution on
the parameters of the differential equation that is the curvature
of the front tire
, and the continuous dependence of the solution on
the parameters of the differential equation that is the curvature
of the front tire 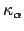 and the initial condition
and the initial condition 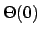 . The existence of a solution for
. The existence of a solution for 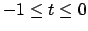 is obtained by comparing the solution
is obtained by comparing the solution 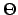 to solutions of the linear equations
to solutions of the linear equations
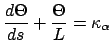
and
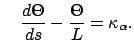
From the continuous dependence on the parameters, it follows that if
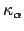 is close to a constant, then
is close to a constant, then 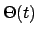 is close to
is close to 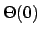 for
for 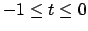 therefore
therefore 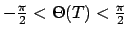 . Furthermore,
. Furthermore, 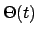 is close to
is close to 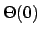 for
for 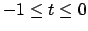 and
and 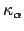 is close to a constant for
is close to a constant for 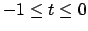 . The iterative nature of our construction then implies
that we should be able to apply the same argument practically indefinitely
as long as we start with a sufficiently small perturbation of a curve
of constant curvature, which can be extended indefinitely. The catch
in this heuristic argument is that the technical meaning of the word
close may change as the iterate along. However, if we start with a very
small perturbation we should be able to extend the curve as far as we
want.
. The iterative nature of our construction then implies
that we should be able to apply the same argument practically indefinitely
as long as we start with a sufficiently small perturbation of a curve
of constant curvature, which can be extended indefinitely. The catch
in this heuristic argument is that the technical meaning of the word
close may change as the iterate along. However, if we start with a very
small perturbation we should be able to extend the curve as far as we
want.
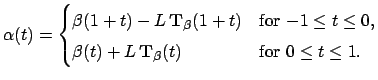
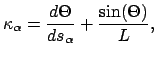
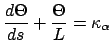 and
and