
Introductory Laboratory Apparatus
Apparatus Title: Physical Pendulum and Damped Simple Harmonic Motion Apparatus
Abstract
We present a variable axis physical pendulum. The pendulum stand includes a bracket for attaching a photogate. To study damped motion, a foam damper is added. A vane attached to the side of the pendulum allows the use of a motion detector to obtain position vs. time data.
Sketch of the apparatus

Figure 1. Physical Pendulum with Stand.
Introduction
This apparatus was designed to meet our need for new labs in simple harmonic and rigid body motion. Our first thought was to design a physical pendulum lab to extend students' experience beyond point masses on massless, frictionless strings. We then realized that the same apparatus could be used for study of damped, undriven simple harmonic motion. The stand designed for the apparatus by our department machinist, Steve Palmer, is versatile enough to use with other equipment. Thus, we now have an apparatus that can be used in several experiments. The pendulum stand is made of aluminum stock mounted to a Formica base. A bracket on the stand supports a photogate. The bracket is in a channel that allows the height of the photogate to be adjusted. The design of the axle allows secure attachment of a spring or simple pendulum to the stand. Removing the axle, we attach a Cenco RodoDyne wheel (model #CP36834-01) to use the stand in an Atwood's machine experiment. The stand is more rigid than the standard post and bench clamp mount, reducing vibrations. Thus, we can use this stand for laboratories on a variety of simple harmonic motion and rigid body motion topics. We present details of the two experiments using the physical pendulum-determining moment of inertia and analysis of damped simple harmonic motion.
Experiment 1: Moment of Inertia of a Physical Pendulum
The first experiment demonstrates a method of determining the moment of inertia of an arbitrary object. By analyzing the torque on a physical pendulum with respect to the rotation axis, we find

In the laboratory, the students measure the period as a function of D. In order to get a best value for the moment of inertia about the center of mass, T2 is plotted against D and fit to equation (4). We use a photogate mounted on the pendulum stand to measure the period, but a stopwatch could be used, as well. Figure 2 shows a graph of typical experimental data.
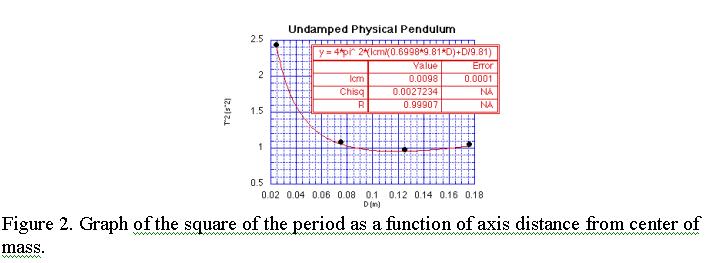
The physical pendulum we designed is a rectangular aluminum plate. We chose to use a regular geometry so students can compare their experimental result to the expected moment of inertia for a rectangle. Four holes are drilled into the plate along an axis of symmetry and fitted with ball bearings to make the pendulum motion as frictionless as possible. The students locate the center of mass experimentally and measure the values for D. They also calculate the moment of inertia the expect for a uniform rectangle with dimensions a x b
Icm=1/12 M (a2+b2). (5)
Experiment 2: Damped Simple Harmonic Motion
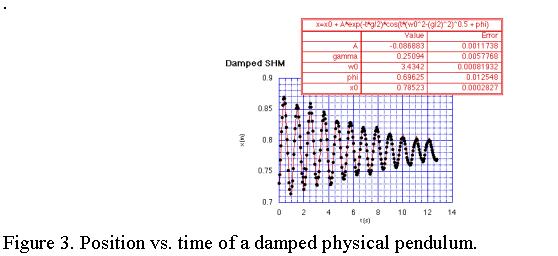
The oscillation of the pendulum may be changed from being virtually frictionless to damped by attaching a foam rubber grommet on the axle just behind the pendulum. The amount of damping adjusts easily by tightening or loosening the screw attaching the pendulum to the axle. To analyze the decaying oscillation of the physical pendulum, we used a Pasco ultrasonic motion detector with the Vernier Universal Laboratory Interface connected to a Macintosh computer running Vernier's MacMotion or LoggerPro software. Since the motion detector "looks" at the thin edge of the pendulum, we attach a lightweight metal vane via a small threaded hole to the side of the pendulum.

A typical experimental result is shown in Figure 3.
Conclusion
We present the design of a physical pendulum that demonstrates very well the dependence on natural period to distance to center of mass. The experimental value for moment of inertia for the rectangular pendulum agrees very nicely with the expected value. The apparatus proves to be very versatile, being used for multiple experiments in simple harmonic and rigid body motion.