Female Income, the Ego
Effect and the Divorce Decision:
Evidence from Micro Data
I. Introduction
During the 1960’s and 1970’s divorce rates in the
This research specifically focuses on the economic causes of divorce. However, there can be little doubt that there are many other factors involved in the decision to dissolve a marriage. For example, demographic factors like changes in the population’s age structure contribute to changes in expected divorce rates. In developed countries where life expectancies have significantly increased, the opportunity for lengthier marriages has also increased. As a natural consequence of a lengthier marriage, the number of divorces would be expected to rise. Development of improved contraceptives and easier access to them has reduced the number of children, thus decreasing the transaction cost to obtaining a divorce. The costliness of children is well known and when a marriage dissolves, the children become an even larger economic burden. Offsetting this burden to a certain degree is the more extensive safety net provided by developed economies. In addition, regime changes like the emergence of no-fault divorce laws have reduced the transaction cost of litigation, and by doing so have increased the likelihood of divorce. Finally, one cannot ignore the personal aspect of the decision to end a marriage. Rapid and extensive societal changes can lead to marriage ending frictions that in other circumstances might well be ignored.
Although the factors mentioned above are clearly of importance, this research concentrates on three economic arguments that have persisted over the years. All three relate to the female’s ability to generate income in the labor market. The first argues that as the female increases her ability to generate income, she becomes financially more independent thereby making divorce more likely. Inextricably tied to this argument is the relative cost of child bearing. As a female’s connection to the labor force strengthens, it increases the transaction cost of child rearing. As a logical consequence, having fewer children reduces the transaction cost of divorce. So, by strengthening ties to the labor force, the female invariably weakens ties to the family. The second argument contends that, as female earnings become a larger share of family income, marital friction results and the likelihood of divorce increases. Finally, it has also been argued that the family unit places a high value on the ability of the married female to earn income and, therefore, strives harder to avoid divorce as the female’s ability to earn income rises.
The remainder of the paper proceeds in five additional parts. The next section of the paper provides a short literature review. It examines both some of the theoretical and some of the previous empirical work dealing with the economic issues of divorce. Part III provides a brief explanation of the statistical model used to accomplish the estimations. Part IV describes the data used in the estimations. Part V discusses the empirical results and, finally, some conclusions and caveats are offered in Part VI.
II. Literature review
Theoretical Models
In their seminal work on marital
instability, Becker, Landes, and Michael [1977] argue that the decision to
divorce compares the value of being single to the joint value of being
married. Following the modeling work of
Weiss [1996], let ![]() be the household
production function that measures the joint value of staying married. This joint valuation is a function of the
characteristics of both spouses,
be the household
production function that measures the joint value of staying married. This joint valuation is a function of the
characteristics of both spouses, ![]() for the male and
for the male and ![]() for the female. The characteristics
for the female. The characteristics ![]() and
and ![]() include the earnings
of each respective spouse. The
production function also includes Kt, which measures
marriage-specific capital such as children.
The final argument in the production function, θt, is an
unobservable measure of the quality of the relationship. All the arguments of the production function
have a subscript “t” to denote a particular time period. The value of these arguments will vary over
the duration of the marriage as will the likelihood of getting a divorce.
include the earnings
of each respective spouse. The
production function also includes Kt, which measures
marriage-specific capital such as children.
The final argument in the production function, θt, is an
unobservable measure of the quality of the relationship. All the arguments of the production function
have a subscript “t” to denote a particular time period. The value of these arguments will vary over
the duration of the marriage as will the likelihood of getting a divorce.
Let the post-divorce value of being
single equal ![]() for the male and
for the male and ![]() for the female. Among other things, these variables include
each spouse’s estimate of the option value of remarriage, a possibility that
occurs only after the current marriage is dissolved. The transactions cost to obtaining a divorce,
Ct, not only includes legal expenses, but it also captures the
opportunity cost of the time lost in divorce negotiations and the emotional
costs incurred during dissolution of the marriage.
for the female. Among other things, these variables include
each spouse’s estimate of the option value of remarriage, a possibility that
occurs only after the current marriage is dissolved. The transactions cost to obtaining a divorce,
Ct, not only includes legal expenses, but it also captures the
opportunity cost of the time lost in divorce negotiations and the emotional
costs incurred during dissolution of the marriage.
Divorce occurs when the sum of the values of becoming single, minus the transaction cost of the divorce, is greater than the joint value of remaining married. Using the terms defined above, divorce is optimal when
![]()
Of primary interest to this research
are the theoretical inferences about income.
For example, an increase in female labor force participation increases
female income, which, in turn, increases ![]() and makes divorce more
likely. Higher female salaries increase
the opportunity cost of children, reduce Kt, and increase the
likelihood of marriage dissolution.
Also, higher female salaries threaten male egos, leading to marital
stress that reduces θt, the quality of the relationship, and
increases the probability of divorce.
and makes divorce more
likely. Higher female salaries increase
the opportunity cost of children, reduce Kt, and increase the
likelihood of marriage dissolution.
Also, higher female salaries threaten male egos, leading to marital
stress that reduces θt, the quality of the relationship, and
increases the probability of divorce.
Empirical Literature
Various empirical studies of divorce in the United States have used a wide assortment of techniques, variables and data to produce results that often appear contradictory and, sometimes even, counterintuitive. In explaining the decision to divorce, cross-sectional, micro-level econometric studies have used independent variables such as marriage tenure; working status of the female; the husband’s earnings, age, and educational level; the wife’s earnings, age, and educational level; the number and age of children; and the occurrence of a previous divorce. Time-series analyses of a country’s divorce rate have used macroeconomic variables such as the unemployment rate, the inflation rate and the rate of growth in real GDP to explain changes in the divorce rate.
Micro, cross-sectional studies
Lombardo [1999], and Greene and Quester [1982] argue that wives facing a higher risk of divorce will hedge against that risk with higher levels of labor force participation, and that they will also respond by working longer hours. The basic argument made in these papers is that investment in nonmarket activities, such as child rearing, becomes relatively less attractive (it yields a lower expected return), and investment in human capital becomes relatively more attractive (it yields a higher expected return) as the probability of divorce increases. Studies by Johnson and Skinner [1986], and Shapiro and Shaw [1983] provide additional evidence for the above argument by finding that women increase their labor force participation prior to dissolution of a marriage. The above papers make a clear causality argument that an increase in the likelihood of divorce increases a female’s willingness to enter the labor force.
Spitze and South in two separate studies [1985, 1986] argue a different line of causality. Their conclusion is that an increase in female labor force participation leads to an increase in familial conflict and, consequently, an increase in divorce. Substantiating evidence for this view is provided by Mincer [1985]. In a survey of twelve industrialized nations he found that rising divorce rates clearly lag rising female labor force participation rates.
Previous studies of the impact of income on divorce have provided mixed results. Becker, Landes, and Michael [1977] find that a rise in expected female earnings increases the probability of divorce, while a rise in expected male earnings reduces the probability of divorce. D’amico [1983] recognizes two distinctly different possible effects of income on divorce. One hypothesis is that as the female’s wage relative to the male’s rises, conflict based on competition for status within the marriage will occur and will increase the likelihood of divorce. The second, opposing hypothesis is the notion that the pursuit of higher socioeconomic status is a familial one and that a wife earning a relatively higher wage than that of the husband may contribute to the overall status goal and solidify the marriage. D’amico’s results tend to confirm the latter hypothesis. Finally, Hoffman and Duncan [1995] find no support for the hypothesis that higher real female wages lead to increased divorce rates and a study by Sayer and Bianchi [2000] tends to confirm this finding.
However, Spitze and South raise another question that is closely related to the income issue. In a 1985 study, they produce evidence that the number of hours a wife works has a greater impact on the probability of divorce than do various measures of the wife’s income.
Macro, time-series studies
In an empirical study of the growth of divorce rates in Great Britain, Smith (1997) finds no evidence that marriage dissolution increases because of the introduction of no-fault divorce laws. He argues that, rather than being the vehicle of change, these types of legal modifications merely codify, react to, and regulate ongoing social and economic transformations. Smith finds that procedural and legal changes do have a powerful, albeit temporary impact. One procedural change that did increase the number of divorces was revised court settlement rules that reduced transactions costs and improved the financial position of females post divorce. Smith attributes the increased number of divorces in Great Britain to rising female labor force participation, higher female income and the subsequent reduction in the female’s economic dependency on marriage. In addition, technological change giving females greater control over fertility has had a significant impact. With improved fertility control resulting in fewer children, a significant transaction cost of divorce has been effectively reduced.
South [1985] finds little evidence that the divorce rate rises during periods of recession and falls during periods of expansion. He does find a positive, albeit small, effect of unemployment on the divorce rate. His model indicates that changes in the age structure and the labor force participation rate of women have significantly stronger impacts on the divorce rate than other macroeconomic variables.
Using a simple vector autoregressive (VAR) approach with macro, time-series data, Bremmer and Kesselring [1999] show that the female labor force participation rate does not Granger cause divorce rates. However, they do provide statistical evidence that divorce rates Granger cause female participation in the labor force. They also show that past participation in the labor market influences women salaries.
In another time-series study using macro data, Bremmer and
Kesselring (2003) use cointegration techniques to investigate the relationship
between divorce, female labor force participation, and median female
income. Though these variables had unit
roots, their first differences were stationary, and these variables were shown
to be cointegrated. Impulse functions
from this model reveal that an increase in divorce leads to a rise in female
labor force participation; but positive innovations to female labor force
participation imply a decline in the divorce rate. Impulse function analysis also shows that a
positive innovation to median female income leads to increased divorce and
increased labor force participation on the part of females.
III. The Statistical Model
The most pervasive thread tying the above literature together is the relationship between female earning capacity and its relationship to divorce. This argument takes several important forms. First is a line of reasoning that developed during the 1970’s and 1980’s when females experienced a substantial increase in their ability to successfully participate in the labor market. Unquestionably, female labor force participation increased during this time and, along with this increase came improved salaries and benefits. Consequently, academics argued that as females developed better access to income outside the marriage the likelihood of divorce increased. While this idea was written about in many ways it proved difficult to quantify. It also led to counter arguments that when a married female’s value in the labor market increased it might well strengthen a marriage and reduce the probability of divorce. The difficulty with quantifying these arguments is the very nature of the observable outcomes. It is possible to observe the income of married females. It is also possible to observe the income of divorced females. Unfortunately, it is not possible to simultaneously observe both outcomes for an individual female. So, while the data may indicate that divorced females participate in the labor force at substantially higher rates than married females, it provides no valid evidence that ready access to the labor market is a causal factor in divorce. In other words, this is a classic sample selection problem.
Over the years, academics of various disciplines began to develop another income related argument that they hoped would explain the increasing occurrence of divorce. As a married female’s contribution to household income grows, it gives her more say in the conduct of the marriage. So, conflict within the marriage is given an opportunity to flourish. Disagreements about the way that money is spent and, for that matter, disagreements over the conduct of everyday household responsibilities become much more likely. However, the sample selection problem arises again. It is possible to observe the amount that married females contribute to the household but it is not possible to directly observe the amount that a divorced female would have contributed to the household had she remained married. Consequently, econometric techniques accounting for these difficulties are required.
A typical statistical approach to solving the above problems begins by specifying a selection equation. For example, the selection equation for the divorce problem would be:
![]()
where![]() represents a vector of variables that predict the likelihood
of divorce. In this case (as in most
cases) the selection variable (
represents a vector of variables that predict the likelihood
of divorce. In this case (as in most
cases) the selection variable (![]() ) is not observed.
Instead, only its sign is observed:
) is not observed.
Instead, only its sign is observed:
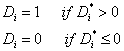
In order to test the above hypotheses regarding divorce, three different income equations need to be estimated. So, there are three equations that will make similar (though not identical) use of the information from the selection equation. The three equations are:
![]()
![]()
![]()
where PY stands for personal earnings and FY stands for family income.
The estimation technique used for all three is very similar. So, model development proceeds by using the first equation as an example. The usual equation that one is interested in estimating is:
![]()
where ![]() is the vector of
independent variables used to predict
is the vector of
independent variables used to predict ![]() . Unfortunately,
. Unfortunately, ![]() is only observed when
is only observed when ![]() =1. Also, for this
derivation the standard assumptions are made about
=1. Also, for this
derivation the standard assumptions are made about ![]() and
and ![]() . In other words, they
have a bivariate normal distribution with zero means and a correlation of r.
. In other words, they
have a bivariate normal distribution with zero means and a correlation of r.
What one truly wishes to estimate is:
![]()
which is equivalent to :
![]() .
.
Incorporation of the selection equation results in the above equation yields:
![]()
![]()
![]()
![]()
where: ![]() . The equation in
estimable form becomes:
. The equation in
estimable form becomes:
![]() .[1]
.[1]
Consequently, application of OLS to
the model results in two problems.
First, omitting ![]() (commonly referred to as the inverse Mills ratio) creates a
bias similar to that attributed to an omitted variable and, second, the
disturbance term,
(commonly referred to as the inverse Mills ratio) creates a
bias similar to that attributed to an omitted variable and, second, the
disturbance term,![]() , is heteroscedastic.
As a result, estimation proceeds in a two-step manner. First, following the methodology recommended
by Heckman [1979], the selection equation is estimated and used to create a
, is heteroscedastic.
As a result, estimation proceeds in a two-step manner. First, following the methodology recommended
by Heckman [1979], the selection equation is estimated and used to create a ![]() for each observation.
Then,
for each observation.
Then, ![]() is estimated by regressing
is estimated by regressing ![]() on
on ![]() and
and ![]() . Finally, the
correction for heteroscedasticity recommended by Greene [1981] is applied to
the estimates. By following similar
logic and making minor adjustments, the estimates for all three of the
equations can be obtained.
. Finally, the
correction for heteroscedasticity recommended by Greene [1981] is applied to
the estimates. By following similar
logic and making minor adjustments, the estimates for all three of the
equations can be obtained.
In order to test the hypotheses specified earlier, an additional step must be taken. It is necessary to use the estimated coefficients obtained from the least squares regressions to produce expected values (observations) for every individual (both married and divorced) in the data set [Lee, 1978]. Once these observations have been obtained, the necessary relationships can be calculated.
The created variable used to test the first hypothesis is:
![]() .
.
Smaller values for ![]() indicate that the
female is better equipped to enter the labor force and, consequently, better
prepared to live independently. If a
female were the only participant in the marriage, it would make sense to argue
that as
indicate that the
female is better equipped to enter the labor force and, consequently, better
prepared to live independently. If a
female were the only participant in the marriage, it would make sense to argue
that as ![]() declines the
likelihood of divorce would definitely increase. However, the male is also a participant in
the marriage and while his interaction in the process has not been written
about as frequently as the female’s, it should (might?) be just as
important. If the male values the
possible economic contribution of the female to the family’s economic welfare,
he would have an increasing preference to remain married as
declines the
likelihood of divorce would definitely increase. However, the male is also a participant in
the marriage and while his interaction in the process has not been written
about as frequently as the female’s, it should (might?) be just as
important. If the male values the
possible economic contribution of the female to the family’s economic welfare,
he would have an increasing preference to remain married as ![]() declines and should,
therefore, seek to reduce the likelihood of divorce.
declines and should,
therefore, seek to reduce the likelihood of divorce.
The other variable of interest is created in the following manner:
![]() .
.
As ![]() declines, the
percentage of total family income accounted for by female earnings
increases. Some authors have argued that
this increasing share of income on the part of the female can cause friction
within the marriage and, consequently, lead to a greater likelihood of divorce. Others have argued that the female’s
contribution could be highly valued by the other family members and should,
therefore, reduce the likelihood of divorce.
So, the question of whether
declines, the
percentage of total family income accounted for by female earnings
increases. Some authors have argued that
this increasing share of income on the part of the female can cause friction
within the marriage and, consequently, lead to a greater likelihood of divorce. Others have argued that the female’s
contribution could be highly valued by the other family members and should,
therefore, reduce the likelihood of divorce.
So, the question of whether ![]() or
or ![]() has a positive or
negative impact on divorce becomes an empirical issue.
has a positive or
negative impact on divorce becomes an empirical issue.
The following equation was formulated to provide a statistical test of these issues:
![]()
where, as before, ![]() stands for divorce.
This equation, estimated by a probit procedure, has been referred to in
the literature as a structural equation [see Lee] because it includes the
specific variables hypothesized to predict the binary outcome. In this particular case, the series of dummy
variables representing the fifty different states is included in the equation
because each state has different laws regarding marriage and divorce. Plus, there are still cultural and social
factors at work in the different states that could lead to varying divorce
outcomes.
stands for divorce.
This equation, estimated by a probit procedure, has been referred to in
the literature as a structural equation [see Lee] because it includes the
specific variables hypothesized to predict the binary outcome. In this particular case, the series of dummy
variables representing the fifty different states is included in the equation
because each state has different laws regarding marriage and divorce. Plus, there are still cultural and social
factors at work in the different states that could lead to varying divorce
outcomes.
IV. The Data
Most of the variables were taken from the March Supplement (Annual Demographic File) of the Current Population Survey. The complete surveys for the years 1990, 1995 and 2000 were obtained from the web site maintained by the National Bureau of Economic Research. State per capita income was obtained from the Bureau of Economic Analysis web site under the heading of State and Local Personal Income. Finally, the Consumer Price Index for 1990, 1995 and 2000 came from the Bureau of Labor Statistics. The names and definitions of all of the variables are provided in Table 1.
The statistical procedures required observations for married females and for divorced females. Application of these restrictions to the data set resulted in 112,740 usable observations. Of this total, 16,760 represented divorced females and 95,980 represented married females.
V. The Statistical Estimations
Table 2 provides the results from the probit procedure that was applied to the divorce selection equation. All variables used in the various estimation procedures were included in this equation. This is the usual procedure for estimations of this type because any variable that affects income should also have an effect on the occurrence of divorce. A criticism that has been directed at models of this type is that unless variables in the selection equation can, reasonably, be excluded from the other equations, results can be unreliable (See Vella, 1998). Fortunately, this formulation of the model provides an entire set of variables that can reasonably be excluded from the income equations—the series of state dummy variables. The state dummies are included in the selection equation to account for differences in state laws and socio-economic conditions that, theoretically, should affect the decision to obtain a divorce. They are excluded from the income equations in favor of state per-capita income. This variable is included in the income equations to account for variation in labor market conditions on a geographical basis.
Due to the rather large number of variables included in the estimation procedure, the coefficients for the state dummy variables (S_), the occupational dummy variables (OC_) and the industry dummy variables (IN_) are omitted.[2] Of the 34 variables listed in Table 2, 28 are significant at the 1 percent or 5 percent level. Most of the variables behaved in predictable ways. For the most part, if the female in question had migrated within the U.S. during the previous year (MIG_), the probability of being divorced was significantly higher. On the other hand, if the migration was from abroad (MIG_ABM, MIG_ABN), the probability of divorce significantly decreased. While the results for the education dummies (ED_) provided some mixed evidence, generally, they indicated that having a lower level of education increases the likelihood of divorce. As family size increases the likelihood of divorce significantly declines and being of Asian descent also reduces the likelihood of divorce. Of course the primary purpose of this equation is not for statistical inference, but for use in estimating the earnings equations.
Table 3 provides the results for the selection corrected estimation of divorced female personal earnings. The coefficients and t-scores for the thirteen occupation dummies and the fourteen industry dummies that were included in the estimation are not displayed.[3] The education variables reveal no significance until the equivalent of a bachelor’s degree is attained. Then the coefficients increase in size and significance as education rises. The estimated coefficients for the migration variables are negative (with one exception) and both of the coefficients that are significantly different from zero are negative. Not surprisingly, the coefficient on being a federal worker is significantly positive while the coefficients on being either a state or a local government worker are significantly negative.[4] Being a member of the labor force significantly increases earnings whether the participant is employed or unemployed. Of the ethnic variables, only the coefficient on being Hispanic is significantly different from 0 (at the 10% level of significance) and it is negative. It is a little surprising that coefficient for age is negative and significant. However, the rest of the variables behave in expected ways. As the number of children in the household increase (Under18), earnings significantly decline. There is also a significant negative relationship between self-employment and earnings. On the other hand, living in a metropolitan statistical area, purchasing a home, increasing levels of state per capita income, and increasing family size all significantly increase earnings. Finally, for this equation, the estimated coefficient for the selection variable (lambda) is negative and significant. The adjusted R-squared for this equation is 0.47 which is a very respectable showing considering that most of the variables used in the equation are binary.
Table 4 presents the estimation results for the selection corrected equation predicting personal earnings for married females. Once again the coefficients and t-scores for the thirteen occupation dummies and the fourteen industry dummies that were included in the estimation are not reported.[5] The results for this equation are very similar to those for the divorced earnings equation. Education doesn’t have a significantly positive affect on earnings until a bachelor’s degree is obtained at which point it has a large impact. Graduate education has an even greater positive effect. Of the six migration variables, only three have significant coefficients and they are all negative. Once again, working for the federal government has a significant and positive impact on earnings, as does participation in the labor force whether employed or not. The estimated coefficients for the ethnic dummies vary considerably from the divorced equation. The coefficients for being African American and Asian are both positive and significantly different from zero at the one percent level. However, the coefficients on being Hispanic or Indian are not significantly different from zero. Once again, age has a significant and negative effect on earnings. The number of children in the household and self-employment both reduce income while living in an MSA, buying a home, having a larger family size, and living in a higher income state all significantly increase earnings. The estimated coefficient for lamda (the selection variable) is negative and significant. Finally, the adjusted R-squared is 0.48.
Table 5 presents the selection corrected results for the equation predicting family income. The coefficients and t-scores for the thirteen occupation dummies and the fourteen industry dummies that were included in the estimation are not reported.[6] The education variables behave in the expected fashion (very similar to the personal earnings equations) with increasing levels of education producing higher levels of income once the high school graduate stage is reached. The migration variables also behave very similarly to the way they behave in the personal earnings equation with a recent migration (within the previous year) resulting in reduced income. The labor force participation variables behave quite differently. If the female is employed it has a positive and significant impact on family income, but if the female is unemployed there is a negative and significant impact on family income. The ethnic variables also behave very differently in this estimation. The estimated coefficients for Black, Indian and Hispanic are all negative and significant. The coefficient for Asian is insignificant. Increasing numbers of children and age significantly decrease family income. Living in an MSA, being self-employed, buying a home, increasing family size, and living in a state with a higher per capita income all significantly increase family income. The estimated coefficient for the selection variable (lambda) is negative and significant. Finally, the adjusted R-squared is 0.38.
Of
course, the final probit provides the most intriguing results and they are
provided in Table 6. Both of the created
difference variables (![]() and
and ![]() ) have negative and significant estimated coefficients. The result for
) have negative and significant estimated coefficients. The result for ![]() indicates that as
females become more successful at producing income in the divorced state, the
more likely they are to become divorced.
The result for
indicates that as
females become more successful at producing income in the divorced state, the
more likely they are to become divorced.
The result for ![]() indicates that as
female earnings becomes a larger portion of total family income, the likelihood
of divorce increases. Interestingly,
the idea that the family attaches a positive value to the female’s earnings and
therefore, attempts to continue the state of marriage fails to overcome the
previous two arguments. There may be
some validity to this contention, but the positive effect (if present) is
obviously not large enough to offset either of the other two effects.
indicates that as
female earnings becomes a larger portion of total family income, the likelihood
of divorce increases. Interestingly,
the idea that the family attaches a positive value to the female’s earnings and
therefore, attempts to continue the state of marriage fails to overcome the
previous two arguments. There may be
some validity to this contention, but the positive effect (if present) is
obviously not large enough to offset either of the other two effects.
In addition to the
two difference variables, the entire series of state dummy variables was included
in this estimation (they are excluded from the individual income equations)
just as it was in the original selection probit (although the results do not
appear in Table 6).[7] The reason for including these variables is
primarily that the various states have different legal systems and, as
mentioned earlier, other studies have found that the legal situation does have
an important impact on the willingness and ability to dissolve a marriage. Curiously enough, 39 of the 50 estimated
coefficients were significantly different from zero at the 10% level of
significance.[8] So, even though the created income
variables (![]() and
and ![]() ) are significant, the geographic dummies retain their
importance. Finally, even though the
structural probit makes use of many fewer variables than the selection probit,
its pseudo R-squared is almost double that of the selection estimation—0.39
compared to 0.22.[9]
) are significant, the geographic dummies retain their
importance. Finally, even though the
structural probit makes use of many fewer variables than the selection probit,
its pseudo R-squared is almost double that of the selection estimation—0.39
compared to 0.22.[9]
VI. Conclusions
The
estimations reported in this paper tend to confirm arguments that have long
been made about the causes of divorce.
As females experience greater levels of success in the labor market,
they also tend to experience higher levels of divorce. This occurs for two important reasons. First, greater financial independence clearly
makes the decision to seek a divorce much simpler. In this respect, developing countries that
have concentrated on guaranteeing equal economic status for females have
reduced the burden of living with unhappy marriages strictly for economic
reasons. However, it also appears that a
female’s economic success may, indeed, cause friction within the family. The results of the estimations in this paper
clearly indicate that as the female’s earnings become a larger portion of total
family income, the likelihood of divorce increases even while controlling for
general success in the labor market (![]() ). Of course, over
time the causes of this effect (fragile male egos?) could well change.
). Of course, over
time the causes of this effect (fragile male egos?) could well change.
Finally, there is little doubt that many other contributory factors affect the decision to seek a divorce. This is the reason that the series of state dummy variables was maintained in the final probit equation. As all statisticians know, resorting to the use of binary variables reveals a certain degree of ignorance. In this particular case, that degree of ignorance turned out to be relatively important, as thirty-nine of the estimated coefficients for the state dummy variables in the final probit were significantly different from zero. In other words, opportunities still exist in the search for a more perfect statistical model of marriage dissolution.
References
Becker, Gary S., Elisabeth M. Landes, and Robert T. Michael, “An Economic Analysis of Martial Instability, “ Journal of Political Economy, 1977, vol. 85, no. 6, 1141-1187.
Bremmer, Dale and Randy Kesslering, “The Relationship between Female Labor Force Participation and Divorce: A Test Using Aggregate Data,” unpublished mimeo, 1999.
Bremmer, Dale and Randy Kesslering, “Divorce and Female Labor Force Participation: Evidence from Times-Series Data and Cointegration,” unpublished mimeo, 1999.
Current Population Survey, March 1990, 1995, 2000 [machine-readable data file] / conducted by the Bureau of the Census for the Bureau of Labor Statistics. --Washington: Bureau of the Census [producer and distributor], 1990, 1995, 2000.
D’amico, Ronald, “Status Maintenance or Status Competition? Wife’s Relative Wages as a Determinant of Labor Supply and Martial Instability,” Social Forces, June 1983, vol. 61, no. 4, 1186-1205.
Duncan, Gregory M., “Sample Selectivity As a Proxy Variable Problem: On the Use and Misuse of Gaussian Selectivity Corrections,” In New Approaches to Labor Unions: Research in Labor Economics, Supplement 2, Edited by Joseph D. Reid, Jr., Greenwich: JAI Press, Inc., 1983.
Greene, William H., Econometric Analysis, Fourth Edition, Prentice Hall, 2000.
Greene, William H., “Sample Selection Bias As a Specification Error,” Econometrica (May 1981), 795-798.
Greene, William H. and Aline Q. Quester, “Divorce Risk and Wives’ Labor Supply Behavior,” Social Science Quarterly, March 1982, vol. 63, no. 1, 16-27.
Greenstein, Theodore N., “Marital Disruption and the Employment of Married Women,” Journal of Marriage and the Family, Aug. 1990, vol. 52, no. 3, 657-677.
Hannan, Michael T., Nancy Brandon Tuma and Lyle P. Groenveld, Income and Independence Effects on Marital Dissolution: Results from the Seattle and Denver Income-Maintenance Experiments,” American Journal of Sociology, 1978, vol. 84, no. 3, 611-633.
Heckman, James J., “Sample Selection Bias As a Specification Error,” Econometrica, vol. 47 (January 1979), 153-161.
Hoffman, Saul and Greg Duncan, “The Effect of Incomes, Wages, and AFDC Benefits on Martial Disruption,” The Journal of Human Resources, vol. 30, no. 1, 19-41.
Johnson, N., and S. Kotz, Distribution in Statistics: Continuous Multivariate Distributions, New York: John Wiley & Sons, 1972.
Johnson, William R. and Jonathan Skinner, “Labor Supply and Martial Separation,” American Economic Review, June 1986, vol. 76, no. 1, 455-469.
Kreider, Rose
M. and Jason M. Fields, "Number, Timing, and Duration of
Marriages and Divorces: 1996", U.S. Census Bureau Current
Population Reports, February 2002.
Lee, Lung-Fei, “Unionism and Wage Rates: A Simultaneous Equations Model with Qualitative and Limited Dependent Variables,” International Economic Review, vol. 19 (June 1978), 415-433.
Lombardo, Karen V., “Women’s Rising Market Opportunities and Increased Labor Force Participation,” Economic Inquiry, April 1999, vol. 37, no. 2, 195-212.
Mincer, Jacob, “Intercountry Comparisons of Labor Force Trends and Related Developments: An Overview,” Journal of Labor Economics, 1985, vol. 3, no. 1, pt. 2, S1-32.
Sayer, Liana C. and Suzanne M. Bianchi, “Women’s Economic Independence and the Probability of Divorce,” Journal of Family Issues, vol. 21, no. 7, October 2000, 906-943.
Shapiro, David and Lois Shaw, “Growth in Supply Force Attachment of Married Women: Accounting for Changes in the 1970's,” Southern Economic Journal, vol. 6, no. 3, September 1985, 307-329.
Smith, Ian, “Explaining the Growth of Divorce in Great Britain,” Scottish Journal of Political Economy, vol. 44, no. 5, November 1997, 519-544.
South, Scott, “Economic Conditions and the Divorce Rate: A Time-Series Analysis of Postwar United States,” Journal of Marriage and the Family, February 1985, vol. 47, no. 1, 31-41.
South, Scott and Glenna Spitze, “Determinants of Divorce over the Martial Life Course,” American Sociological Review, August 1986, vol. 51, 583-590.
Spitze, Glenna, and Scott South, “Women’s Employment, Time Expenditure, and Divorce,” Journal of Family Issues, September 1985, vol. 6, no. 3, 307-329.
Stanley, T.D. and Stephen B. Jarrell, “Gender Wage Discrimination Bias? A Meta-Regression Analysis,” The Journal of Human Resources, Fall 1998, vol. 33, no. 4, 947-973.
Vella, Francis, “Estimating Models with Sample Selection Bias: A Survey,” The Journal of Human Resources, Winter 1998, vol. 33, no. 1, 127-169.
Weiss, Y. “The Formation and Dissolution of Families: Why Marry? Who Marries Whom? And What Happens Upon Divorce?” Handbook of Population and Family Economics. M.A. Rosenweig and O. Stark, eds. Elsevier: North Holland, 1996.
Table 1
List of Variables
|
Variable |
Definition |
|
S_[two
letter state code] |
Binary:
1 for selected state, 0 otherwise (Washington,
D.C. is included) |
|
ED_56 |
Binary:
1 if highest grade attempted was fifth or sixth, 0 otherwise |
|
ED_78 |
Binary:
1 if highest grade attempted was seventh or eighth, 0 otherwise |
|
ED_9 |
Binary:
1 if highest grade attempted was ninth, 0 otherwise |
|
ED_10 |
Binary:
1 if highest grade attempted was tenth, 0 otherwise |
|
ED_11 |
Binary:
1 if highest grade attempted was eleventh, 0 otherwise |
|
ED_12 |
Binary:
1 if highest grade attempted was twelfth, 0 otherwise |
|
ED_Hsgd |
Binary:
1 if high school graduate, 0 otherwise |
|
ED_Univ |
Binary:
1 if some college was attempted, 0 otherwise |
|
ED_BA |
Binary:
1 if college graduate, 0 otherwise |
|
ED_Grad |
Binary:
1 if some graduate school was attempted, 0 otherwise |
|
OC_Exec |
Binary:
1 if executive, 0 otherwise |
|
OC_Prof |
Binary:
1 if Professional, 0 otherwise |
|
OC_Tech |
Binary:
1 if Technician, 0 otherwise |
|
OC_Sales |
Binary:
1 if Sales, 0 otherwise |
|
OC_Clerical |
Binary:
1 if Clerical and administrative support, 0 otherwise |
|
OC_Household |
Binary:
1 if Household service worker, 0 otherwise |
|
OC_Guard |
Binary:
1 if Protective service worker, 0 otherwise |
|
OC_Oservice |
Binary:
1 if Other service worker, 0 otherwise |
|
OC_Craft |
Binary:
1 if Craft and repair worker, 0 otherwise |
|
OC_Machine |
Binary:
1 if Machine operator, 0 otherwise |
|
OC_Transport |
Binary:
1 if Transportation and material moving, 0 otherwise |
|
OC_Equipment |
Binary:
1 if Handler, equipment cleaners, etc., 0 otherwise |
|
OC_Farm |
Binary:
1 if Farming, forestry and fishing, 0 otherwise |
|
IN_Ag |
Binary:
1 if Agriculture, 0 otherwise |
|
IN_Mine |
Binary:
1 if Mining, 0 otherwise |
|
IN_Construction |
Binary:
1 if Construction manufacturing, 0 otherwise |
|
IN_DGS |
Binary:
1 if Durable goods manufacturing, 0 otherwise |
|
IN_NDGS |
Binary:
1 if Non Durable goods manufacturing, 0 otherwise |
|
IN_Trans |
Binary:
1 if Transportation, communication and public utilities, 0 otherwise |
|
IN_Whtr |
Binary:
1 if Wholesale trade, 0 otherwise |
|
IN_Retr |
Binary:
1 if Retail trade, 0 otherwise |
|
IN_Fin |
Binary:
1 if Finance, Insurance or Real Estate, 0 otherwise |
|
IN_Bserv |
Binary:
1 if Business and repair services, 0 otherwise |
|
IN_Pserv |
Binary:
1 if Personal services, 0 otherwise |
|
IN_Ent |
Binary:
1 if Entertainment and recreation services, 0 otherwise |
|
IN_Profs |
Binary:
1 if Professional and related services, 0 otherwise |
|
IN_Padm |
Binary:
1 if Public administration, 0 otherwise |
|
MIG_MM |
Binary:
1 if Migrated from MSA to MSA in previous year, 0 otherwise |
|
MIG_MNON |
Binary:
1 if Migrated from MSA to non MSA in previous year, 0 otherwise |
|
MIG_NONM |
Binary:
1 if Migrated from non MSA to MSA in previous year, 0 otherwise |
|
MIG_NN |
Binary:
1 if Migrated from non MSA to non MSA in previous year, 0 otherwise |
|
MIG_ABM |
Binary:
1 if Migrated from abroad to MSA in previous year, 0 otherwise |
|
MIG_ABN |
Binary:
1 if Migrated from abroad to non MSA in previous year, 0 otherwise |
|
WC_Fed |
Binary:
1 if Worked for federal government, 0 otherwise |
|
WC_Local |
Binary:
1 if Worked for local government, 0 otherwise |
|
WC_State |
Binary:
1 if Worked for state government, 0 otherwise |
|
LF_Work |
Binary:
1 if Working, 0 otherwise |
|
LF_Unemp |
Binary:
1 if Unemployed but in the labor force, 0 otherwise |
|
Black |
Binary:
1 if African American, 0 otherwise |
|
Indian |
Binary:
1 if American Indian, 0 otherwise |
|
Asian |
Binary:
1 if Asian, 0 otherwise |
|
Hispanic |
Binary:
1 if Hispanic, 0 otherwise |
|
Age |
Age
of the individual measured in years |
|
Under18 |
Number
of children under 18 years of age living with the family |
|
MSA |
Binary:
1 if living in an MSA, 0 otherwise |
|
Selfemploy |
Binary:
1 if Self employed, 0 otherwise |
|
Homebuy |
Binary:
1 if Purchasing the home, 0 otherwise |
|
Statepcy |
Per
capita income of the state of residence |
|
Famsize |
Number
of people in the family |
|
1995 |
Binary:
1 if Observation is from 1995, 0 otherwise |
|
2000 |
Binary:
1 if Observation is from 2000, 0 otherwise |
|
Divorce |
Binary:
1 if Divorced, 0 otherwise |
|
Fincome |
Family
income measured in constant dollars |
|
Pincome |
Personal
income measured in constant 1982-1984 dollars |
Table 2
Estimation Results for the
Probit Selection Equation
(dependent variable =
Divorce)
|
Variable |
Coefficient |
t-score |
|
Constant |
0.1509 |
0.732 |
|
ED_56 |
-0.1522 |
-2.324** |
|
ED_78 |
0.0642 |
1.117 |
|
ED_9 |
0.1505 |
2.494** |
|
ED_10 |
0.1864 |
3.254* |
|
ED_11 |
0.1403 |
2.432** |
|
ED_12 |
0.1420 |
2.020** |
|
ED_Hsgd |
0.1072 |
2.104** |
|
ED_Univ |
0.1847 |
3.577* |
|
ED_BA |
-0.0445 |
-0.830 |
|
ED_Grad |
0.0675 |
1.206 |
|
MIG_MM |
0.0578 |
3.547* |
|
MIG_MNON |
0.0904 |
2.004** |
|
MIG_NONM |
-0.1364 |
-2.542** |
|
MIG_NN |
0.2473 |
8.365* |
|
MIG_ABM |
-0.4063 |
-5.572* |
|
MIG_ABN |
-0.5810 |
-2.192** |
|
WC_Fed |
0.0293 |
0.720 |
|
WC_Local |
0.0138 |
0.576 |
|
WC_State |
0.0801 |
2.531** |
|
LF_Work |
0.2836 |
6.397* |
|
LF_Unemp |
0.3325 |
6.267* |
|
Black |
0.4260 |
21.769* |
|
Indian |
0.3022 |
5.695* |
|
Asian |
-0.4105 |
-10.159* |
|
Hispanic |
0.0427 |
2.158** |
|
Age |
0.0134 |
27.633* |
|
Under18 |
0.7474 |
92.804* |
|
MSA |
0.1631 |
10.171* |
|
Selfemploy |
-0.2555 |
-11.475* |
|
Homebuy |
-0.5600 |
-43.586* |
|
Statepcy |
-0.0000 |
-1.185 |
|
Famsize |
-0.9525 |
-125.417* |
|
1995 |
0.1055 |
7.305* |
|
2000 |
0.1649 |
4.895* |
|
|
|
|
|
n |
112,740 |
|
|
Chi
squared (goodness
of fit) |
28,632.46* |
|
|
Pseudo
R sqared (Mckelvey
and Zavoina) |
0.2243 |
|
*Significant at the 1% level.
**Significant at the 5% level.
Table 3
Estimation Results for the
Divorced Personal Income Equation
(dependent variable =
Personal Earnings)
|
Variable |
Coefficient |
t-score |
|
Constant |
-5938.062 |
-3.961* |
|
ED_56 |
414.453 |
0.363 |
|
ED_78 |
376.520 |
0.349 |
|
ED_9 |
-229.585 |
0.838 |
|
ED_10 |
-568.008 |
-0.467 |
|
ED_11 |
-481.276 |
-0.434 |
|
ED_12 |
-173.434 |
-0.144 |
|
ED_Hsgd |
398.550 |
0.376 |
|
ED_Univ |
846.582 |
0.785 |
|
ED_BA |
3840.904 |
3.595* |
|
ED_Grad |
7318.364 |
6.680* |
|
MIG_MM |
-511.214 |
-2.705* |
|
MIG_MNON |
-880.202 |
-1.609 |
|
MIG_NONM |
-1537.966 |
-2.486** |
|
MIG_NN |
-533.094 |
-1.470 |
|
MIG_ABM |
651.284 |
0.631 |
|
MIG_ABN |
-219.384 |
-0.051 |
|
WC_Fed |
1994.064 |
4.281* |
|
WC_Local |
-1099.755 |
-3.716* |
|
WC_State |
-960.939 |
-2.600* |
|
LF_Work |
5402.567 |
8.594* |
|
LF_Unemp |
1444.790 |
2.105** |
|
Black |
-395.019 |
-1.534 |
|
Indian |
-194.288 |
-0.331 |
|
Asian |
611.861 |
1.140 |
|
Hispanic |
-443.722 |
-1.865*** |
|
Age |
-26.624 |
-2.883* |
|
Under18 |
-1071.602 |
-3.753* |
|
MSA |
1358.628 |
6.372* |
|
Selfemploy |
-836.517 |
-2.624* |
|
Homebuy |
2068.368 |
8.241* |
|
Statepcy |
0.360 |
11.251* |
|
Famsize |
780.981 |
2.134** |
|
1995 |
224.029 |
1.290 |
|
2000 |
27.884 |
0.149 |
|
Lamda
(IMR) |
-1423.519 |
-2.689* |
|
Rho |
-0.164 |
|
|
n |
16,760 |
|
|
F |
241.95* |
|
|
Adjusted
R2 |
0.471 |
|
*Significant at the 1% level.
**Significant at the 5% level.
***Significant at the 5% level.
Table 4
Estimation Results for the
Married Personal Income Equation
(dependent variable =
Personal Earnings)
|
Variable |
Coefficient |
t-score |
|
Constant |
-6415.416 |
-17.545* |
|
ED_56 |
-284.100 |
-0.991 |
|
ED_78 |
-1.920 |
-0.007 |
|
ED_9 |
-238.122 |
-0.827 |
|
ED_10 |
-374.250 |
-1.327 |
|
ED_11 |
-507.512 |
-1.832** |
|
ED_12 |
-336.782 |
-0.979 |
|
ED_Hsgd |
-345.321 |
-1.423 |
|
ED_Univ |
82.323 |
0.334 |
|
ED_BA |
2028.300 |
8.007* |
|
ED_Grad |
6270.188 |
23.618* |
|
MIG_MM |
-14.550 |
-0.175 |
|
MIG_MNON |
-98.368 |
-0.440 |
|
MIG_NONM |
-997.990 |
-3.654* |
|
MIG_NN |
-297.523 |
-1.966** |
|
MIG_ABM |
-1112.558 |
-3.962* |
|
MIG_ABN |
77.786 |
0.101 |
|
WC_Fed |
2428.852 |
11.379* |
|
WC_Local |
-749.226 |
-6.593* |
|
WC_State |
84.579 |
0.525 |
|
LF_Work |
5197.963 |
27.379* |
|
LF_Unemp |
1513.559 |
6.089* |
|
Black |
748.609 |
6.650* |
|
Indian |
134.426 |
0.482 |
|
Asian |
793.503 |
5.587* |
|
Hispanic |
13.274 |
0.149 |
|
Age |
-11.689 |
-4.758* |
|
Under18 |
-529.507 |
-10.081* |
|
MSA |
915.309 |
13.491* |
|
Selfemploy |
-931.276 |
-9.990* |
|
Homebuy |
1277.754 |
16.798* |
|
Statepcy |
0.300 |
24.607* |
|
Famsize |
92.319 |
1.744** |
|
1995 |
461.506 |
7.190* |
|
2000 |
679.873 |
9.799* |
|
Lamda
(IMR) |
-621.565 |
-3.027* |
|
Rho |
-0.795 |
|
|
n |
95980 |
|
|
F |
1450.42* |
|
|
Adjusted
R2 |
0.484 |
|
*Significant at the 1% level.
**Significant at the 5% level.
Table 5
Estimation Results for the
Married Family Income Equation
(depedent variable = Family
Income)
|
Variable |
Coefficient |
t-score |
|
Constant |
-21996.904 |
-10.538* |
|
ED_56 |
305.502 |
0.218 |
|
ED_78 |
429.783 |
0.301 |
|
ED_9 |
157.097 |
0.107 |
|
ED_10 |
98.911 |
0.058 |
|
ED_11 |
487.994 |
0.333 |
|
ED_12 |
2023.786 |
1.305 |
|
ED_Hsgd |
4495.666 |
3.138* |
|
ED_Univ |
7822.660 |
5.430* |
|
ED_BA |
15525.113 |
10.604* |
|
ED_Grad |
21973.639 |
14.962* |
|
MIG_MM |
-1156.044 |
-5.255* |
|
MIG_MNON |
384.954 |
0.659 |
|
MIG_NONM |
-3809.466 |
-5.389* |
|
MIG_NN |
-1897.787 |
-4.740* |
|
MIG_ABM |
-4557.808 |
-6.199* |
|
MIG_ABN |
335.830 |
0.168 |
|
WC_Fed |
512.926 |
0.935 |
|
WC_Local |
-2357.779 |
-8.045* |
|
WC_State |
-1963.318 |
-4.740* |
|
LF_Work |
3099.166 |
6.306* |
|
LF_Unemp |
-1434.980 |
-2.240** |
|
Black |
-5554.957 |
-19.133* |
|
Indian |
-3469.821 |
-4.842* |
|
Asian |
298.584 |
0.802 |
|
Hispanic |
-4286.220 |
-16.786* |
|
Age |
-320.324 |
-40.466* |
|
Under18 |
-7449.363 |
-49.628* |
|
MSA |
4869.148 |
26.902* |
|
Selfemploy |
2363.281 |
9.798* |
|
Homebuy |
10163.315 |
49.171* |
|
Statepcy |
1.118 |
35.063* |
|
Famsize |
8795.796 |
49.702* |
|
1995 |
-1372.387 |
-8.270* |
|
2000 |
-325.845 |
-1.832** |
|
Lamda
(IMR) |
-8807.076 |
-14.156* |
|
Rho |
-0.434 |
|
|
n |
95,980 |
|
|
F |
962.07* |
|
|
Adjusted
R2 |
0.383 |
|
*Significant at the 1% level.
**Significant at the 5% level.
Table 6
Estimation Results for the
Structural Probit
(dependent variable =
Divorce)
|
Variable |
Coefficient |
t-score |
|
Constant |
-0.10681 |
-0.913 |
|
|
-0.00014 |
-16.978* |
|
|
-0.00016 |
-121.822* |
|
|
|
|
|
n |
112,740 |
|
|
Chi squared (goodness of fit) |
54,877.90* |
|
|
Pseudo R sqared (Mckelvey and Zavoina) |
0.385 |
|
*Significant at the 1% level.