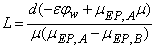ME497
Microfluidis

 RHIT ME Home Dr. Thom's Homepage
  RHIT
Main Page		 ME
Homepage		 Dr. Thom's
Homepage

Catalog Description: (Prerequisites - CHEM 201 or equivalent) Gives general introduction to the field of microfluidics. Introduction to fluid mechanics at the microscale: electroosmotic flow, eletrophoresis, chemical separation and detection, microfluidic device fabrication, and microchannel heat exchangers.

Small channels, big fun.



Contract
Calendar
Homework
Communication
Gradebook
Other stuff
Homework
Assigments   Hints   Solutions    

HW 1

Problem Hint Answer
     
     

Back to Top | Back to Assignments

HW 3

Problem Hint Answer
Prob 2 Be very careful with units here. Do not assume everything works out. Some intermediate answers:
b2=57.5 μm
n=5.17×1025 m-3

Back to Top | Back to Assignments

HW 4

Problem Hint Answer
1. The key is that ideal mixing (at least here) means that the entire mass of each gas fills the entire volume. Also realize that the incoming density is different than the density of that species inside the volume. The mass of each species changes exponentially.
2. You will have to integrate here, taking into account that the velocity changes with each r. I would set up an integral with a differential element dA that has r in it. Uin = U0/2

Back to Top | Back to Assignments

HW 5

Problem Hint Answer
2.A straight forward macroscopic mass and linear momentum application problem. Don't forget that linear momentum has a direction.

It may look like there are two streams leaving the plate, but there is in fact only one. V2 is in the radial direction, not the y direction.

 
3.The solution to this may look trivial to you, but it is of importance to us later on, at least conceptually.  
4.Just follow the same method as in 3. and you'll be OK.  

Back to Top | Back to Assignments

HW 6

Problem Hint Answer
2. Remember that vectors have direction and magnitude, not just magnitude.  
3. "Using what your know about the properties of linear ordinary differential equations" means being able to use l_n_a_r _up_rp_si_t__n.  
4. Assume that disassociated KCL (i.e K+ and Cl- ions) make up the charge carriers in the electrolyte.  
5.
  1. For the minimum length, where would the detector be located? Where would this minimum distance between mitochondria plugs occur, then?

    Don't forget that the electrophoretic mobility helps you find the velocity relative to the bulk flow. You therefore need an expression for the bulk flow velocity also.

  2. We're using the same concepts here as in part a.
a. 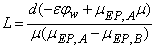P-12_4_a_ans.gif
b. 31.4 mV (-31.4 mV)
c.1 mm/s, 59 s

Back to Top | Back to Assignments

HW 8

Problem Hint Answer
1. This is an example of how an otherwise complicated heat transfer problem can be reduced to a very simple problem. I suggest you draw two thermal resistors in series and label the voltages (temperatures). Now you need only solve a V1 - V2 = IR problem. You just have T instead of V and Qdot instead of I  
3. For part c, there is more than one correct result, as the correlations are experimental. Parts a and b have just one correct result each. Part d is for a few extra points!  

Back to Top | Back to Assignments

HW 9

Problem Hint Answer
1. The handout in class is a template for this problem. The one in class was actually harder, as the EOF velocity profile is much simpler, isn't it? Nu=constant, where 10<constant<20 (The constant is just one value, but I don't want to give too much away.)
2.

Take it one step at a time, and all should be well.

To get the numbers listed here, fluid properties should be ρ=998 kg/m3, η=0.001 kg/m-s and κ=0.603 W/m-C°. If you use different values, you will get slightly different answers.
  1. 1.568×10-4 kg/s
  2. 23.06°C
3.Be careful with your areas. Both tubes contribute to the overall heat tranfer area. Also, both tubes contribute to the total mass flowrate for your energy balance.
  1. Re=141, Nu=3.66
  2. h=3121 W/m2-°C, Ts=36.01°C

Back to Top | Back to Assignments