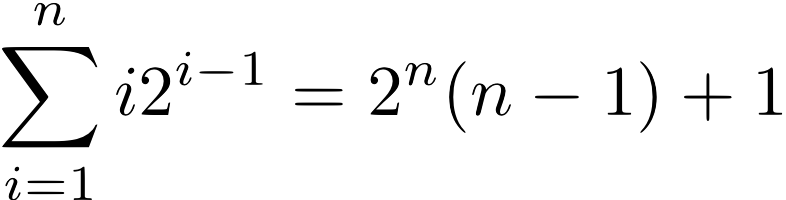CSSE 230
Data Structures and Algorithm Analysis
Homework 4 - 40 points
Reading (optional)
In our textbook, read 6.3 - 6.8 (the zybooks "assignment" called "Reading for HW4").
The authors do a couple things differently than we do.
First, they use while loops to traverse a tree path. It's a valuable technique to know about, but you'll notice
that we present recursion in lecture.
Why? Recursion is more general, from algorithms that only need to visit one path up to those that need to visit
the entire tree.
And recursive code is simpler, especially when you use you use the NULL dummy node and approaches that avoid
parent pointers.
So we'll require you to use recursion whenever possible, recognizing that things like iterators still require
loops.
Second, instead of static functions, we implement our algorithms in methods that have access to
this because that more closely follows
the object-oriented paradigm used in practice.
They also present general BSTs which allow duplicates while we'll focus on using trees to implement the Set
interface (so no duplicates).
To Be Turned In
The first few are to be submitted to the drop box and the last one committed to your repository through github
classroom. If either part (dropbox or repo) is late, you will be charged a late day.
If both parts are early, you can gain a late day
-
(20 points) Calculate the exact average-case
time complexity of binary search. You may use any standard implementation of binary search,
e.g., textbook, wikipedia, etc.
Only consider successful searches (where the item we are looking
for is actually in the array) and assume all elements are equally
likely to be the one we are searching for.
- Complete this for N=7 elements in the array.
- Complete this for N=15 elements in the array.
- Complete this for N = 2k
- 1 for some integer k
≥ 0, generalizing from what you found in (a) .
Hint: For each i, count how
many of the array elements will be found after binary search examines exactly i array elements. (For
example, the middle element is the only one to be found after examining one array element, and there are two
elements that can be found after examining two array elements.) Then sum over all and divide to find the
average. For the generalization, you'll use a
summation. You need to convince me somehow that your summation is
correct, perhaps using a table or words. Once you have done that, then
you may find the following formula useful:
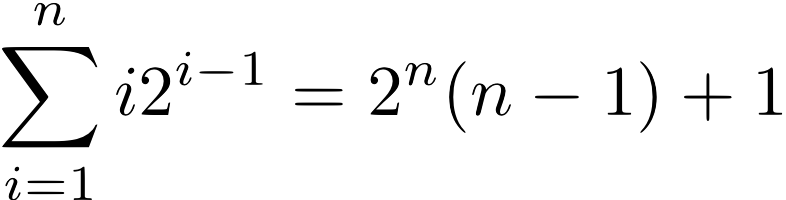
After you have done that, you'll get a messy expression with lots of terms in it. Take the limit as n gets
large so some terms go to zero. You'll end up with a much simpler expression that should be clearly
between 1 and log(n), like we said in class.
The interesting question we are trying to answer here is how much smaller is the average-case analysis
compared to the worst case analysis you can find in your text- book.
- (20 points) Accept the TreePractice
project from the following link.
Complete the exercises, per the given
specifications, and commit your solutions back to the repository.
These are good practice for exams. Recall the recursive pattern from
day 7. Strategy as the recursive problems get more complicated: on
some problems, you will want to communicate
information down the tree as you recurse, so you will find it
helpful to add a parameter to your recursive method. You may also use
objects as return values to return multiple things up the tree - we'll explore that a LOT in the homework 5
tree practice.