CSSE 230
Data Structures and Algorithm Analysis

Homework 8  - 36 points

Reading

(Towards the Reading grade) In our textbook (link at top of Moodle page), read 9.1-9.6.

This reading is mostly about graph applications, which complements the lectures nicely. Additionally, section 9.9 may be usefu to you when doing GraphSurfing Milestone 2.

To receive full credit, complete the self-quizzes as you go. (You can re-take any you don't get correct the first time; you are graded on your participation.) The reading is a zybooks "assignment" called "Reading for HW8".

To Be Turned In

Submit to the drop box.

  1. (16 points) For this problem, consider the two main ways of implementing a graph: adjacency lists, or adjacency matrix.
    1. Of the two implementations, which would be more efficient at removing an edge from the graph? Explain your answer by describing what must be done in each of the two implementations, and giving the asymptotic running times.
    2. Of the two implementations, which would be more efficient at removing an vertex from the graph? Explain your answer by describing what must be done in each of the two implementations, and giving the asymptotic running times.
  2. (20 points) In this problem, we consider completely full binary trees with N nodes and height H 
                      (so that N = 2H+1 – 1 )
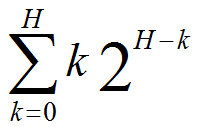
    (a) (5 points) Show that the sum of the heights of all of the nodes of such a tree can be expressed as       SumOfHeightsSummation

    (b) (15 points) Prove by induction on H that the above sum of the heights of the nodes is N - H - 1.  You may base your proof on the summation from part (a) (so you don't need to refer to trees at all), or you may do our "standard" binary tree induction based on the subtrees (using the definition that a non-empty binary tree has a root plus left and right subtrees). We find the tree approach more straightforward, but you may use the summation if you prefer.