CSSE 230
Data Structures and Algorithm Analysis

Homework 2 (58 points)

To Be Turned In

Upload your solution to the Moodle drop box. See submission instructions in HW1.   After you have submitted, click on the uploaded submission to verify that your submission was successful.

A single late day may be used or earned for each homework assignment: you must turn in all parts early to earn a late day; if you turn in any part late, you will use a late day.

Problem numbers [in square brackets] are the numbers from the 3rd edition of the Weiss book.

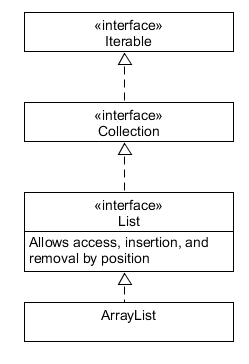
1. (10 points) Using the official javadoc, draw a UML diagram of the Collections framework. Add whatever notes you find helpful. Include at least these classes/interfaces: ArrayList, Collection, ConcurrentSkipListSet, HashSet, Iterable, LinkedHashSet, LinkedList, List, PriorityQueue, Queue, Set, SortedSet, Stack, and TreeSet. These are the main ones; we skipped most of the concurrent/blocking structures, and some special-purpose ones. Note that the map ADT (AbstractMap, TreeMap, and HashMap) aren’t connected to the others: they form their own hierarchy that is so close to that for Sets, that it isn't worth you writing (although we expect you to know and use Maps). Hints: 1. Most relationships are that of an interface extending or a class implementing an interface - use dotted lines there. There is only one example of inheritance - use a solid arrow there. 2. A class may implement multiple interfaces - there is one example of that here. 3. Here is the top of the hierarchy - copy this pic and skim each of these interfaces and class in the javadoc to get started. 4. I just started with the ArrayList javadoc and looked for the required classes/interfaces (finding Iterable, Collection, and List), and then looked at each of those to see which one was a subinterface and which was a superinterface. 5. Feel free to do this with a partner, but you must each submit one copy.   

2. (8 points). Use the formal definition of big-Oh (see Weiss section 5.4) to show that 2N² + 3N + 8 is O(N²). That is, find appropriate constants N₀ and c, and show that they work.
3. (12 points) Weiss Problem 5.3[5.3], parts a–d. For each of these statements: if the statement is always true, explain why using the N₀ and c idea from the formal definition of big-Oh. [Hint: the given bounds on T₁ and T₂ tell you something about the existence of an N₀ and c for each of those functions: we could call these numbers N₀₁, c₁, N₀₂, and c₂] If the statement can be false, give an example of functions T₁ T₂, and F for which it is false. (Hints: For algorithm analysis we assume that all the functions have non-negative values; an algorithm can’t execute in negative time.  Note that the use of big-O instead of big-theta here is intentional; some of the answers would be different if big-theta was used instead.)
4. (6 points) In asymptotic analysis, it's very useful to know if the base of a logarithm mattters.
   1. Is it true that log₂(n) is θ(log₁₀(n))? Justify your answer. (Hint: use one of the logarithm formulas!)
   2. Is it true that 10ⁿ is θ(2ⁿ)? Justify your answer.
5. (12 points) For each of the following four code fragments, similar to Weiss problem 5.20 [5.15], first give the exact number of times the "sum++" statement executes in terms of n. Then use that to give a Big-Theta running time (by ignoring the low-order terms).

   1. for (int i=0; i <= n+2; i++) {
         for (int j=0; j < n * n; j++) {
             sum++;
         }
      }

   2. for (int i=0; i < n; i++) {
         for (int j=i; j < n; j++) {
             sum++;
         }
      }

   3. You may assume that n is a power of 2.

      for (int i = n; i > 0; i /= 2) {
         for (int j = 0; j < i; j++) {
             sum++;
         }
      }
      

   4. for (int i=n; i >= 1; i = i / 2) {
         sum++;
      }

6. (10 points) Weiss Exercise 5.30 [5.23]. Note that your method is supposed to efficiently search the sorted (increasing) array a of integers, looking for an integer i for which a[i] == i and return true if and only if there is such an i.

   You may assume that the array has no duplicate entries, and therefore is strictly increasing. I.e. a[j-1] < a[j] for all j with 0 < j < a.length. You may not assume that all of the integers in the array are non-negative, because then the problem would be boring.

   Show your algorithm and the results of your analysis. Obviously you should try to come up with an efficient algorithm; some of the credit for this problem will be based on your algorithm's efficiency. (Think about it carefully—is O(N) "efficient" for this task? Anyone can write a loop from 0 to a.length.)

For Your Consideration

These problems are for you to think about and convince yourself that you could do them. It would be good practice to actually do them, but you are not required to turn them in.

• Weiss Exercise 6.5 [6.5]. (You may have to come back to it a few times before you figure out what to do.) Here is a more detailed explanation:

  The goal of this problem is to implement a collection data type that provides three operations and does them efficiently:

  push(obj); // adds obj to the collection.
  
  obj = pop(); // removes and returns the most recently-added object.
  
  obj = findMin(); // returns the smallest object (assume that all
   // of the objects in the collection are Comparable).
  

  A single stack can do the first two operations in constant time, but not the third. But if our implementation uses TWO stacks to represent a collection, it is possible to do each of the three operations in constant time. Is should be obvious that our new data structure’s push method will have to do more work (than the push operation for an ordinary stack would have to do) in order for findMin to also be a constant-time operation. All you need to do is show the code for the three operations. You may assume that there is already a Stack class that has its own push, pop, and top methods. The code for each of the three methods that you must provide is short. We hope that by making things a bit more specific, it will make it easier for you to get started on this problem.

  To further assist you in understanding this problem, here is a framework in which your answers could go: A class declaration with stubs for the three methods you are supposed to write. Each of those methods should be constant time (no loops or recursion)

  public class StackWithMin<E> {
   // TODO: Give these two stacks names indicating what they are used for:
   private Stack<E> stack1, stack2;
  
   public StackWithMin() {
   this.stack1 = new Stack<E>();
   this.stack2 = new Stack<E>();
  }
  
   public void push(E element) { /* TODO: fill in the details */ }
   public E pop() {/* TODO: fill in the details */ }
   public E findMin() {/* TODO: fill in the details */ }
  }
  

• Weiss exercises 6.26(a)(b), 6.27(a)(b), 6.28(a)(b) [6.12(a)(b), 6.13(a)(b), 6.14(a)(b)]. No implementation required; just the algorithm and analysis.