CSSE 230
Doublets
Objectives
-
Practice with polymorphism, Collections, Maps, Sets, Queues, Stacks, and
Priority Queues.
- Experimenting with search strategies and efficiency
(depth-first, breadth-first, and A*) via choice of data structures.
- Practice writing algorithms.
Partners
You should
plan to use pair programming for all of your coding/debugging work. Certainly you
can split up the tasks of learning about things you need for this
program, but you should write all of the code together.
If both partners have remaining a late day, you may use a late day for
this assignment.
After the project is due, each of you will evaluate your partner;
often both partners will receive the same grade, but if these
evaluations or any other info make us think it is appropriate, we may
give you different grades.
Overview
In 1879, Lewis Carroll (author of Alice in Wonderland and Through
the Looking-Glass, among other classics), documented a word puzzle
he termed "Doublets," which you may have seen. He wrote:
DEAR VANITY [FAIR], -Just a year ago last Christmas, two
young ladies-smarting under that sorest scourge of feminine humanity,
the having "nothing to do"-besought me to send them "some
riddles." But riddles I had none at hand, and therefore set myself
to devise some other form of verbal torture which should serve the
same purpose. The result of my meditations was a new kind of Puzzle-new
at least to me-which, now that it has been fairly tested by a year's
experience and commended by many friends, I offer to you, as a newly-gathered
nut, to be cracked by the omnivorous teeth which have already masticated
so many of your Double Acrostics.
The rules of the Puzzle are simple enough. Two words are proposed,
of the same length; and the Puzzle consists in linking these together
by interposing other words, each of which shall differ from the next
word in one letter only. That is to say, one letter may be
changed in one of the given words, then one letter in the word so
obtained, and so on, till we arrive at the other given word. The letters
must not be interchanged among themselves, but each must keep to its
own place. As an example, the word "head" may be changed into
"tail" by interposing the words "heal, teal, tell, tall."
I call the two given words "a Doublet," the interposed words
"Links," and the entire series "a Chain," ...
It is perhaps, needless to state that it is de rigeuer that
the links should be English words, such as might be used in good society.
...
I am told that there is an American game involving a similar principle.
I have never seen it, and can only say of its inventors, "pereant
qui ante nos nostra dixerunt!"
Your task in this assignment will be to build the underlying data
structures that will allow you to find a chain of links yielding a
solution to Carroll's doublets for any pair of words. In the next
assignment, you'll complete the search algorithm and do some preliminary
experiments with it.
Suggested Incremental Development Path
The following incremental steps may help you to get there. You are not
required to take this path.
You can find the starting code in the Doublets project in your pair's SVN repository.
Milestone 1: Links
Your first task is to build a data structure that represents the allowable
links for each word. For example, we should be able to efficiently
determine that the candidate plays from heal include heel,
hell, heat, heap, real, hear, deal,
zeal, seal, peal, head, veal, and
meal, while the candidates from glass are grass,
glads, class, gloss.
Create a class called Links that contains such a structure.
The constructor should take a file name as a parameter and call a
private helper method to populate the links data with word information
from the file, which should have one word per line. Include a member
method, getCandidates(), that takes a string and returns a collection of the valid connections
(i.e., candidate plays) from the given word or null if there
are none.
The getCandidates() method in Link must execute in O(1) time. It gets
called OFTEN when searching for doublets. For example, it should
probably just do an O(1) lookup into a data structure and then check to
see if it should return null – most importantly, it can't do any string
calculations. Therefore, you will need to do all of the work to figure
out the set of words that differ from the given word in the
constructor.
- Note:
- Building this structure may have
a high time complexity. However, the structure itself should facilitate
the low complexity operations that will be necessary to play the game.
- Optional (perhaps later):
- Because creating the links is a high-cost startup operation, you may
want to modify Link so that it is serializable. Then you
may write the processed word list to disk and load the object directly
on the fly.
Make sure your code passes the given tests. This milestone will be graded separately.
When you complete Milestone 1, be sure to commit it with a message like
“MILESTONE 1 DONE” so that we know which version to grade (we assume
that once you finish milestone 1, that you’ll continue working and
committing other versions). This is important to calculating early/late
days on Milestone 1.
Data
You can find several word list files (derived from SCOWL)
in your repository. The number in the file name indicates the frequency percentile of
the word usage. Thus, english.cleaned.10.txt is a shorter list,
but its words are more common than those who appear (additionally)
in english.cleaned.all.20.txt., or english.cleaned.all.35.txt.
The lists are supposed to be strict subsets of
one another.
Milestone 2: Everything Else
Chains
Create a class Chain representing an immutable sequence of link words.
Recall that immutable just means that after the data is initialized in
the constructor, no method may change any fields. It should support adding a new word to the
(end) of the chain, as well as retrieving the last word in the chain
(i..e., to see if it is the desired word). Because the objects are
immutable, adding a word should construct and return a new Chain.
Your class should be an Iterable<String>, so that you can
easily look over the contents (in order) and ultimately print the
solution. Include a length method as well.
When searching for a chain between the doublets, it will be important
not to repeat any words (otherwise your solution will be unnecessarily
long). Thus, to ensure your chain does not repeat words, you should
include a boolean method contains to determine efficiently
whether a given word appears in the chain.
- Note:
- You can do this with the collection
types we have studied. However, for optional code economy, examine
the Java Collections framework for a single collection
data structure that does nearly everything required.
Managing Chains
Starting from the first doublet, there are many possible links that
could lead to a solution. For instance in finding a valid chain for
Carroll's doublet from head to tail, you may decide
to use a link from head to heal, or you might decide
instead to use a link from head to hear.
Which one should you choose? If you are playing cerebrally, you might
choose the link that seems most promising. However, it could end up
being a dead-end, requiring you to resort to some alternative link.
Computationally, this process requires storing the alternatives you
intend perhaps to try later if your search should come up short. Of
course, you'd also need a method to retrieve one of those alternatives
for examination. This should sound much like the capabilities of two
collections you have studied recently featuring slightly different
spins on "put one in" and "take one out" capabilities.
Because the behavior can differ, we may want to use them interchangeably
to guide our search.
You can visualize the search as a tree:
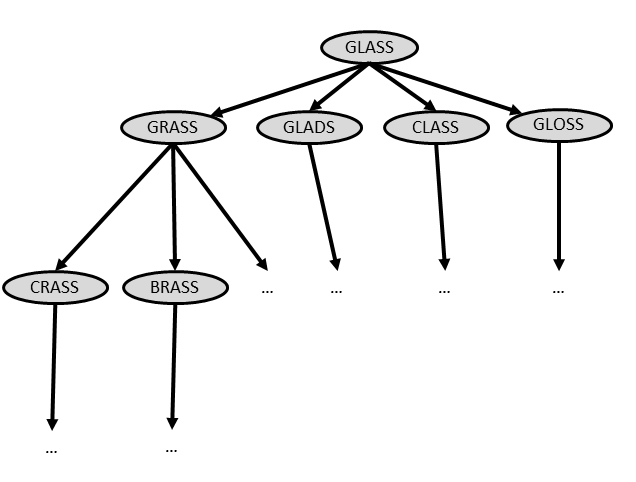
GLASS has 4 links to candidate words. GRASS has 2 links shown.
Searching for the correct chain just means expanding this tree until we
find the end word. This makes sense if we can expand words in parallel.
But we can't do this; we can only call getCandidates() on one word at a
time. So we need to store the other chains in some kind of data
structure.
Say we wanted to call getCandidates() to examine all the words at depth
= 1 first before looking at anything on level 2: this is called a
breadth-first search. (Can you see why? We search broadly before we go
deep along a path.) What kind of traversal did we call this? What kind
of data structure did we use for the corresponding iterator?
But maybe we think a depth-first search would be quicker. Then we would want
to call getCandidates() on the first chain at depth 1 (grass), then call
getCandidates() on the first new candidate at depth 2 (crass), then
getCandidates() on the first new candidate in level 4, etc. all before expanding
any of the other chains at depth 1! What kind of traversal is this? What kind of
data structure did we use for the corresponding iterator?
See the difference? In the first case, we expand GLADS before CRASS, but in
the second, we expand CRASS before GLADS.
Abstract Class
To take advantage of polymorphism, we have given you a ChainManager
abstract class that supports two core methods: add, which simply
adds a chain for future consideration, and next, which
returns (and removes) a chain.
In addition to these, we may be interested in tracking the performance
of the manager. We include two other methods, numNexts, which
returns the number of times next has been called, and maxSize,
which returns the the largest number of chains the manager has stored
so far.
Implementations
Create two implementations of ChainManager, one called QueueChainManager
that treats chains in a FIFO fashion, and another called StackChainManager
that treats chains in a LIFO fashion. The next method should
return null when there are no more chains left to consider.
- Note:
- java.util.LinkedList IS-A
java.util.Queue. Your QueueChainManager
implementation should only use Queue methods.
Doublet Chain
With all of the pieces in place from the previous assignment, you
are now ready to find a chain of links between doublets. But
how? A sketch of the algorithm is as follows.
To get the process started, the initial chain is quite simple: it
should contain the start word. This is your current (first) candidate
chain.
What should you do with a candidate? First, see whether the last word
in the chain is the ending doublet. If it is, the candidate chain
is in fact a solution. Otherwise, you'd need to get the allowable
linking words of the candidate chain's last word. (This is what you
built earlier in the assignment.)
For each of these possible linking words, you'd tell the chain manager
that you'd (later) like to consider a new chain (built on the candidate)
that has the linking word at the end. Of course, that's only if the
linking word is not already in the candidate chain.
Once you've done that, you'd ask the chain manager for the next chain
to consider and repeat the process. If the chain manager says there's
nothing left, you know there is no chain between the doublets.
Create a class called Doublets whose constructor takes a
Link object. Add a member method getChain that
takes the two doublet strings (starting and ending) and a ChainManager,
returning a solution Chain or null if there is none.
This method should implement the algorithm sketched above.
Interactive Program
Use all of these pieces to create an interactive program (main
in Doublets) that allows you to specify the word file at
start up. It should repeatedly prompt the user for a doublet and provide
the chain solution or an appropriate message if there is none. Report
the solution length, the number of candidate chains examined (i.e. number of
times next called), and
the maximum size of the candidate pool (maximum size of the specific chain
mamager's stack, queue, ...). For example, using english-words.35.links,
-
Welcome to Doublets, a game of "verbal torture."
Enter starting word: flour
Enter ending word: bread
Enter chain manager (s: stack, q: queue, x: exit): s
Chain: [flour, floor, flood, blood, bloom, gloom, groom, broom, brood, broad, bread]
Length: 11
Candidates: 16
Max size: 6
Enter starting word: wet
Enter ending word: dry
Enter chain manager (s: stack, q: queue, x: exit): q
Chain: [wet, set, sat, say, day, dry]
Length: 6
Candidates: 82651
Max size: 847047
Enter starting word: oat
Enter ending word: rye
The word "oat" is not valid. Please try again.
Enter starting word: owner
Enter ending word: bribe
Enter chain manager (s: stack, q: queue, x: exit): s
No doublet chain exists from owner to bribe.
Enter starting word: cold
Enter ending word: warm
Enter chain manager (s: stack, q: queue, x: exit): x
Goodbye!
Consider a More Efficient Manager!
You have likely found that using a stack to
manage the search is akin to following a chain all the way to completion
first, no matter how long it may be. Conversely, using a queue to
manage the search is like trying (and remembering!) every possible
link at every possible stage. In this way, a queue unfolds the search
into large tree of possibilities that expands layer by layer until
you find a solution or no possibilities remain.
The stack manager tends to find chains that are unnecessarily long.
Meanwhile, the queue manager is guaranteed to find the shortest solution,
but can take gobs of memory. Both of these managers somewhat unintelligently
choose which candidate to explore next. Can we perhaps do better?
When new chains are added to a queue, they are necessarily at the
end. Thus the queue manager returns the candidate with the shortest
chain for examination. While this is an advantage, when several chains
have the same length, we have no way of distinguishing which may be
better. For instance, which of the following two chains would you
prefer to be working from for the doublet head/tail?
head-held-hell-hall-hail
head-heat-feat-fear-pear
If you've played the game before, you'd probably pick the first. Why?
After five moves, the end of the first chain differs from the goal
word by only a single character. By contrast, the end of the second
chain differs from the goal word in all four characters. We have an
intuitive sense that the first is better. Can we formalize this somehow?
Instead of returning the shortest chain for examination, we would
like to return the chain with the shortest total estimated solution
length. That is, when a particular incomplete chain is extended to
yield a solution, what will the solution's length be? We already know
how long the candidate chain is, but how can we estimate how much
longer the chain must be to reach the solution? One optimistic estimate
is to count the number of characters that differ between the chain's
end and the goal word. Because you can only change one character at
a time, the remaining chain must have at least this many words in
it (though perhaps more).
The value of a chain (for a particular doublet) is thus given by
|
Value=Length+Differences, |
|
where "Differences" means the the number of characters
that differ between the goal word and the end of the chain.
In this assignment, you'll create a new chain manager that efficiently
returns the most promising chain for consideration in the search;
that is, the one with the lowest value. Will this strategy improve
our situation? We will find out!
Priority Queue Chain Manager
If you hadn't already guessed, one of the most efficient ways to keep
a collection of things and quickly access the "best" is a priority
queue. In this part, we will build up a PriorityQueueChainManager
that implements the ChainManager interface. You can begin
by creating a skeletal implementation.
Java's PriorityQueue uses the elements' so-called "natural
ordering", which is revealed by the compareTo method. That
means the items it stores must be Comparable. To this point,
you've likely been storing items inside the stack and queue as Chains.
However, these are not comparable. While it might make sense to compare
chains by their length, our new manager will require that we compare
candidate chains by their total estimated length.
One might argue that a chain is independent of a solution or even
the doublets or the search strategy; it is just a sequence of words.
Your prior managers knew nothing about the doublets, chain length
(explicitly), or even the search they played a part in. Because we
might use estimation methods other than the one outlined above, the
estimated total length is something that should be the chain manager's
responsibility for calculating. In addition, it is often true in real-world
practice you are handed classes and objects and you cannot change
them. Consider that to be the case here: the Chain class
simply cannot be modified.
Constructor
Add a constructor to your PriorityQueueChainManager class
that takes the ending word as a parameter (which should then be a
member of your class).
Distance Estimate
Add a private method to your PriorityQueueChainManager class
that takes a string and returns the number of characters that differ
from the target string. It may take as a precondition that the strings
are the same length.
Entry Class
Because chains are not directly comparable using their length, we must
create a new composite type to store in the priority queue. This new
type will use a combination of the chain's lengths and their "distance
from target", as defined above, as the basis
of its natural ordering.
Create an inner class of PriorityQueueChainManager called
Entry. Its constructor should take a Chain as a
parameter, calculate and store the total value of that chain using
its length and your distance estimate, as outlined above.
The class should implement Comparable using the total value
as the basis for comparison.
Use Your New Chain Manager
You should now be able to complete the implementation of your priority
queue-based chain manager. A call to next should always return
the chain that has the lowest value (length plus differences).
Augment your Doublets program so that it can now use the new search
strategy as an option.
That is, your program asks:
Enter chain manager (s: stack, q: queue, p: priority queue, x: exit): p
PS: once you finish this part, you will have implemented a cornerstone of artificial
intelligence (AI): A* search! http://en.wikipedia.org/wiki/A*_search_algorithm (PPS,
further along this tangent: In Dr. Boutell's solution of LodeRunner in CSSE220, his
Guards used A* search to find the best path to pursue the Hero.)
Provided Code
To enable you to focus on the non-routine parts of this program, we have
provided you with a small amount of starting code and two test classes.
In ChainManager.java,
we have given you a basic framework and some variable declarations that you may find helpful.
Feel free to change anything except the signature of the methods, since we may write test
code that calls these directly. You may wish to write additional methods
to help with your computations.
There are unit tests for the Link and Chain classes, which are some of the
first you'll need to write. After that, you'll test it with your program.
Practical Notes
Recall that the Java option -Xmx allows one to specify the maximum heap
size available to the program. You will likely need to increase this
from Java's paltry default in order to do actual searches with the
given links files. See here for a reminder about how to do this.
Turn-in Instructions
Turn-in your programming work by committing it to your SVN repository.
(Of course, you should have committed many times by now). Be sure that
your code contains the name(s) of the author(s).
Grading
We plan to use this checklist: GradingChecklist_Doublets.doc
Credits
This assignment was created by Rose CS/MA alumnus (2001) Jerod Weinman,
who is now a professor at Grinnell College. Modifications
and solution by Matt Boutell and
Claude Anderson. The excerpts of Lewis Carroll, published by Vanity Fair in
1879, are in the public domain.

