CSSE 230
Data Structures and Algorithm Analysis
Written Assignment 8 - 37 points
To Be Turned In
Submit to the drop box.
-
Don’t forget: You should be keeping an individual log about your team project work so that you can write a performance evaluation for each of your teammates. You do not need to turn in this log, but I wanted to remind you while I had your attention.
-
(deleted)
-
(15 points). Weiss Exercise 19.7. Prove it by
strong induction on the size of the tree. The induction assumption applies to the left
and right subtrees.
This exercise is based on the discussion
from pages 644-647 (beginning of section 19.3) and Exercise 19.
I restate it in terms of Extended Binary Trees (EBTs), because
the definition is a bit more precise than the one in the middle
of page 647. An EBT T either consists of one external node, or
it consists of an internal node (the root) and two subtrees, TL
and T,
each of which is an EBT. See the in-class PowerPoint slides from
day 13 for more details. If T is an EBT, then its
internal path length,
IPL(T) is the sum of the depths of all of the internal nodes of
T. Similarly, its
external path length,
EPL(T) is the sum of the depths of all of the external nodes of
T.
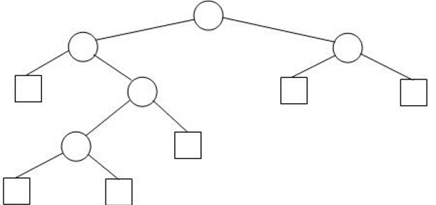
For example, if T is the EBT shown below, then IPL(T) =
0+1+1+2+3 = 7, EPL(T) = 2+2+2+3+4+4 = 17. Note that, since N=5
in this example, the formula is indeed true. Your job is to show
that it is true for all extended binary trees.
Based on this definition of EBTs, use strong induction to show
that for any non-negative integer N and any EBT T that contains
N internal nodes, EPL(T) = IPL( T) + 2*N. Be sure that you
explain what you are doing. You may introduce any new notation
that may be helpful.
-
(deleted)
-
(12 points) Solve the recurrence relations below. Indicate which strategy you are using and show your work. Big-theta or exact answer required? Big-theta.
On any problem where it is appropriate to use the Master Theorem, big-theta is sufficient (you can't get better from the theorem).
But if the master theorem doesn't apply for a certain problem (hint, hint), you'll have to use another technique like telescoping,
or filling out a table and doing guess and check.
And then you'll have an exact answer anyway on your way to getting big-theta. So write the exact answer too as part of your solution.
-
T(1) = 1, T(N) = 2 T(N/4) +
N0.5
-
T(1) = 1, T(N) = T(N
- 2) + 2, assuming
N
is odd.
-
T(1) = 1, T(N) = 3 T(N/2) + 2N
-
(10 points) Use a recurrence relation to show that the running time of the
printPreorder
method in Figure 18.22 is O(N). You may assume that the tree is perfect (i.e., full, balanced, and size 2k
- 1 for some integer
k).
