-
3.14 * 3.14 - 1/2 -
LOG(218,2) -
A1 * A2 >= B1 * B2
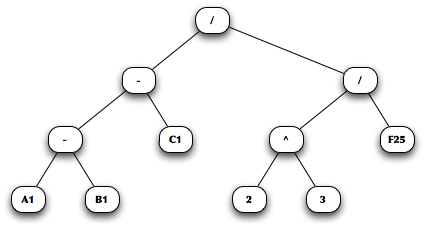
(11 points) Give the expression represented by the expression tree below. Include parentheses as necessary so that your expression matches the evaluation order implied by the tree.
(15 points) This problem is based on Weiss Exercise 19.19, but I’m rewriting it here to clarify some things and eliminate part of the exercise. You may do this as a pencil-and-paper exercise, or you may try to get it working in code. If you do the latter, please turn in a print out of the code you write.
Implement a static, factory method for
BSTreeWithRank
that takes two indices,
low
and
high, and constructs an optimally balanced
BSTreeWithRank
that contains all the integers between
low
and
high, inclusively. (The signature of the method is given below.) All leaves should be at the same level (if the tree size is 1 less than a power of 2) or on two consecutive levels.
Your routine should run in linear time. No partial credit will be awarded for solutions that do not run in linear time.
For example, calling
BSTreeWithRank.buildRangeTree(4,12)
would yield a tree with 9 nodes and root element
8. Calling
findKth(0)
on that tree would yield
4. Calling
findKth(8)
would yield
12.
Assume the
BSTreeWithRank
and
BNodeWithRank
implementations that we developed in class and that were shared in the
BSTWithRankSolution
project in SVN.
This method can be implemented using a recursive helper method. Below is the required method, plus a stub for the recursive helper method. You just need to give the details of the helper method. Be sure to show how the
rank
of each node is set, as well as how it is connected to the rest of the tree.
public static BSTreeWithRank<Integer> buildRangeTree(int low, int high) {
BSTreeWithRank<Integer> result = new BSTreeWithRank<Integer>();
result.root = recursivelyBuildRangeTree(low, high);
return result;
}
private static BNodeWithRank<Integer> recursivelyBuildRangeTree(int low, int high) {
// TODO Write the details
}