CSSE 230
Pascal's Christmas tree (100 points)

Objectives

Overview

The following picture appears in the University of Chicago School Math Project's high-school book Functions, Statistics, and Trigonometry:
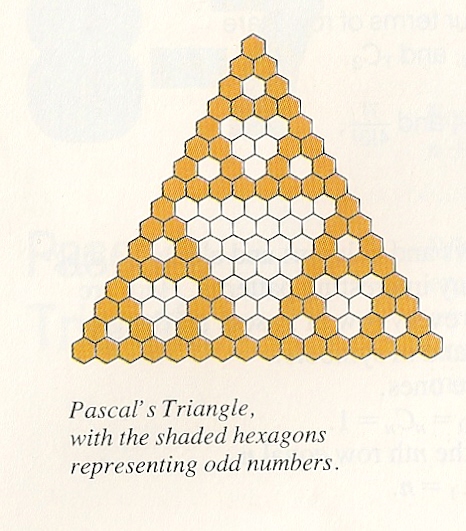
Pascal Triangle Diagram from HS textbook
You will write a program that draws pictures like this. If you use green for odd numbers and red for even, the picture will resemble the title of the assignment.  For an introduction to Pascal's Triangle, see http://en.wikipedia.org/wiki/Pascal_triangle .

Consider which rows do not contain any even numbers.  They are rows 0, 1, 3, 7, 15, ...  Then consider this table that maps k to the corresponding "all odd" row:
k r(k) = corresponding row with only odd numbers
0 0
1 1
2 3
3 7
4 15

Your program should prompt the user for a number k≥2 and a window height, and then pop up a window on which it draws the shaded triangle of regular hexagons whose last row is r(k).   Ideally, your triangle should fit in the window for any k, but making it perfect is not easy.  It should certainly fit in the window for larger values of k (say, k>=4), but may overlap a little for k=2 and/or k=3.  

Adjusting the triangle to be centered and to mostly fill the window is one of the most difficult parts of this assignment, and so it will have a non-trivial impact on your score.

That's all! But this task is easier said than done.  There are several places along the way where you are likely to encounter snags.  Each of those is an opportunity for you to learn something and adjust your approach.

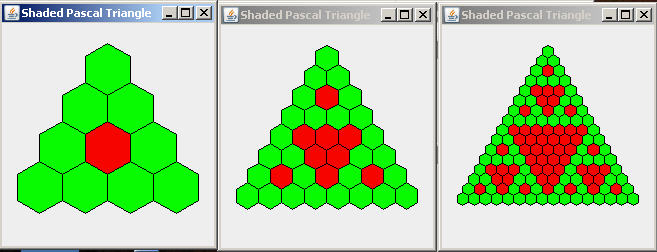
The following examples show the results for k=2, 3, and 4 and a small window size.  Notice that for a given window size, the triangle is the same size for each k; the hexagon size gets smaller as k gets larger k.
THree pascal triangle images

You can find the starting code in the PascalChristmasTree project in your pair's SVN repository. 

Partners

Your instructor will tell you who your partner is and the name of that repository. You should plan to use pair programming for all of your coding/debugging work.  Certainly you can split up the tasks of learning about things you need for this program, but you should write and debug all of the code together.  We recommend tat the partner who feels least sure about programming in Java be the most frequent driver in your pair-programming sessions. 

If both partners have remaining a late day, you may use a late day for this assignment.

After the project is due, each of you will evaluate your partner; usually both partners will receive the same score, but if these evaluations or any other info make us think it is appropriate, we may give you different grades.

Suggested Incremental Development Path

The following incremental steps may help you to get there.  You are not required to take this path; the only deliverable is a well-written, well-documented program that produces the correct pictures.  If you follow this path, our best guess is that step 6 is the halfway point in the time required to write and debug this assignment.
  1. Write a static method combinations() that computes the ith entry of row j, which is jCi, the number of different combinations of j distinct items, taken i at a time. One well-known formula for this is j(j-1)...(j-i+1) / i!.  The following example shows a computation order that may be preferable:  12C4 = 12 / 1 * 11 / 2 * 10 / 3 * 9 / 4.  Note that for all nonnegative integers i ≤ j,  when the formula for the number of combinations is evaluated in this order, each intermediate value in the above computation is an integer, and the numbers you have to deal with are smaller than if you calculate the numerator for the factorial formula and then divide by the denominator.  Of course you will need a loop to do this computation.  [Option:  You can speed up the computation considerably by storing previously-computed value(s) and using them to compute the next value, using the formula for an element of Pascal's Triangle that involves adding the two elements above it in the triangle.  That is not required for this assignment.  Can you think of other ways to speed up the computation?].   Test your method.
  2. Write nested loops to print Pascal's triangle to the console. Don't worry about formatting, except that you should get the correct numbers in the correct order for each row.
  3. Create a graphical program that repeatedly draws some shape (it doesn't matter what shape) in a centered triangular pattern.  This is a "for practice only" program.
  4. Write a static method  that produces and returns a regular hexagon Shape that can by drawn or filled by a Graphics2D object.  Our suggestion is that you produce a Path2D.Double object instead of a Polygon object, because the latter can have coordinates that are not integers.  The moveTo() and lineTo() methods of the Path2D.Double class may be useful.  At what angle from the x-axis should the first vertex be in order to draw hexagons that are oriented like the ones in the pictures?  We found that the following signature made the method easy to implement:
       public Path2D.Double hexagon(double centerX, double centerY, double radius)
    Test your method by drawing some hexagons. Draw a row of contiguous regular hexagons across the screen.  What is the relationship between the width of a hexagon and its radius?
  5. Draw a second row of hexagons below the first, positioning them so that they form the honeycomb pattern as in the pictures. As a function of the hexagon radius, what is the vertical distance between the top of one row and the top of the row below it?
  6. Determine the rectangular area in which the triangle is to be drawn, based on the window width and height and the minimum inset you want to have around the triangle. Then, based on k, determine the radius of the largest hexagons that you can use to draw the triangle inside this rectangle. 
  7. Draw the triangle of hexagons, containing the correct number of rows, based on k.  Test it for k=2, 3, and 4. 
    Note that there is some commented-out code that draws a horizontal line at the midpoint of the window.  Uncommenting this line and running the code can provide a check to see if you really have the triangle centered in the window.
    Also note that there seems to be a minimum window width, so if you you call the constructor with a very small second argument, the triangle will be the correct size, but the window will be "too wide", so the triangle will not be centered.
  8. Before you draw each hexagon, fill it with the correct color, based on the parity of the corresponding value in Pascal's triangle.
  9. Try larger values of k. Does your code still work?  If not, fix it. For a height 750 window, our pictures look good and draw instantly up through k=8.  For k=9, it takes a few seconds to draw, and the hexagons are so small that the black lines of their borders begin to obscure the red and green.  For k=10 (1024 rows of the triangle), the hexagons are so small that the black borders fill the entire triangle; it takes more than a minute to draw it unless we use a very efficient algorithm; an efficient algorithm can do it in a couple of seconds.  Your code should work for any value of k, although it only has to have good-looking pictures for up to k=8.
  10. Commit the project to your repository often.  Be sure that your code contains both authors' names.

Provided Code

To enable you to focus on the non-routine parts of this program, we have provided you with some starting code.  You should read and understand (ask if you don't understand) the code in PascalViewer.java, but you should not have to change it at all.  In PascalComponent.java, we have given you a basic framework and some variable declarations that you may find helpful. Feel free to change anything except the signature of the constructor, since we may write test code that calls the constructor directly without using the code in PascalViewer.java. You may wish to write additional methods to help with your computations.

Prohibition

You may not use a 2-dimensional array in your code.   Doing so would require a lot of space, and it is unnecessary.  Everything can be calculated one row at a time.

Turn-in Instructions

Turn-in your programming work by committing it to your SVN repository.    The grading rubric/checklist is available here: GradingChecklist_PascalChristmasTree.doc

Start early

A few pairs may finish this program in one or two sessions together.     But many pairs will need multiple sessions over several days in order to get his done.