Instructor info
| Instructor |
Claude Anderson |
| Office Phone |
877-8331 |
| Office Address |
F210 (Northeast corner, top floor of Moench)
(not important for summer online course) |
| Office Hours |
I expect to be available in my
office most weeks MTR 1:00-4:30, W10:00-4:00, and F 1:45-3:30. Many days I will
also get to my officee earlier in the afternoon and stay until 5:00 or a bit
later. You can make an appointment or "drop in". My
Outlook Calendar is public. |
| E-mail |
anderson@rose-hulman.edu
or
csse474staff@rose-hulman.edu (staff address is not for summer) |
Schedule
page
(bookmark it in your browser) and other online resources |
http://www.rose-hulman.edu/class/csse/csse474/201420/Schedule/Schedule.htm
This is where I will post readings, assignments, resources, exam dates,
etc.
Some things
that are interactive or that I do not want to post publicly (such as
solutions to HW or quizzes) will be posted on the Moodle course page.
Announcements and discussion forums on
Piazza. |
Required Text

Automata, Computability, and Complexity: Theory and Applications
by Elaine Rich (Prentice Hall, 2008)
The author has a companion web site:
http://theoryandapplications.org/
Approximate reading schedule (I will adjust this as we go along)
| Session 1-4 |
(0.5 weeks) |
Math Review, Languages and Computation, FSM intro. |
Appendix A (read before course begins)
Chapters 1-4
|
| Sessions 5-14 |
(2.5 weeks) |
Finite State Machines, Regular languages |
Chapters 5-10 |
| Sessions 15-24
|
(2.5 weeks) |
Pushdown Automata, Context-Free Languages |
Chapters 11-16 |
| Sessions 25-34
|
(2.5 weeks) |
Turing Machines, Undecidability |
Chapters 17-26 |
| Sessions 35-40
|
(1.5 weeks) |
Complexity, Applications |
Chapters 27-28
Appendices G-Q (selections) |
Other Books
- A book that I recommend for every Computer Scientist's library:
Grimaldi, Ralph P. Discrete and Combinatorial Mathematics
(Addison-Wesley, 2003)
- Other good books on Automata and Computation:
- Introduction to Automata Theory, Languages, and Computation by Hopcroft, Motwani, and Ullman (Addison-Wesley, 2001)
- Introduction to the Theory of Computation by Michael Sipser (Thomson
Course Technology-Hill,
2006)
- Languages and Machines by Thomas A. Sudkamp (Addison-Wesley, 2004)
Course Description
RHIT Catalog Description
Students study
mathematical models by which to answer three questions: What
is a computer? What limits exist on what problems computers
can solve? What does it mean for a problem to be hard?
Topics include models of computation (including Turing
machines), undecidability (including the Halting Problem)
and computational complexity (including NP-completeness).
Course Learning Outcomes (adopted by CSSE department,
September 2009)
Students who successfully complete this course should be
able to:
- Explain the concepts of finite automata and regular languages.
- Design deterministic and nondeterministic automata to recognize specified regular languages.
- Design regular expressions to generate specified regular languages.
- Explain the concepts of context-free and context-sensitive grammars.
- Design context-free grammars to generate specified context-free languages.
- Design push-down automata to recognize specified context-free languages.
- Design Turing Machines to recognize languages and compute functions; explain the significance of the Universal Turing machine.
- Explain the Church-Turing thesis and its significance.
- Determine a language's location in the Chomsky hierarchy (regular, context-free, context-sensitive, recursively enumerable languages).
- Prove that a language is in a specified class and that it is not in the next lower class.
- Convert among equivalently powerful notations for a language, including among DFAs, NFAs, and regular expressions, and between PDAs and CFGs.
- Explain why some problems have no algorithmic solution.
- Provide examples that illustrate the concept of undecidability
- Prove that a problem is undecidable by reducing a classic known undecidable problem to it.
- Define the classes P and NP.
Prerequisites
CSSE 230 Data Structures and Algorithms MA 375 Discrete and Combinatorial Algebra II
| | Note: The course
actually depends much more on MA
275 than on CSSE 230 or MA 375. If you are very
comfortable with the contents of chapters 2-7 of Grimaldi's book,
and if mathematical induction is "second nature" to you, you should
be fine. If not, you may have to work extra-hard in this
course for the first few weeks. The MA 375 exposure to
finite state machines will also be helpful, but we will take a
slightly different approach
in this course. |
Appendix A of the textbook contains a review of most of the material you
should know from those courses, some of it in slightly more depth than Ralph Grimaldi's book (for example, first-order logic).
In addition, you should know the basics of Finite State Machines (Grimaldi
Chapter 6 and Section 7.5), although the perspective on FSMs in this course will
be a bit different.
The main things that you should bring into this course
- enthusiasm, curiosity, perseverance, and a "can do" attitude, especially
concerning proofs and mathematical terminology (if you don't pay attention to
terminology, you're dead in this course!)
- willingness to work cooperatively with other students in the classroom to enhance the learning environment for everyone
- determination to consistently devote enough time to the course
- commitment to read the textbook and get all you can from it, so that more
class time can be spent on problem solving
- commitment to avoid getting behind, and to ask questions when you don't understand something
- a reasonable comfort level with elementary discrete mathematics (especially
proofs). Appendix A of the Rich book is a good benchmark. If you
came to the course already comfortable with about 70% of that appendix, you should be fine.
Assignments (quizzes, Homework, etc.)
Some days there will be in-class note
sheets,
similar to in-class quizzes in other CSSE courses.
You will not be required to
turn these in. I will provide solutions for some of
them. When I give a reading assignment,
I seriously expect you to read it.
In-class discussions will assume that you have done the reading
and understood the "easy stuff" before class. Sometimes there will be
reading quizzes based on the
definitions and simple concepts form a reading assignment.
You may of course ask about any details that you do
not understand. When there is a reading quiz, you must submit a hard copy at the beginning of class. You can print it and write
on it, or do it electronically and then print it.
I will assign many written problems, most of them from the textbook. These will
typically be short
thought problems, mathematical analyses, formal proofs, or machine-design
exercises. I expect you to think through them carefully and write your answers
legibly and clearly (if you prefer, type them and print them). On some problems,
not only the correctness but also the quality of your solution will determine
your grade. Some of the problems will be straightforward practice with concepts
from the course; others will require creative solutions. Don't put them off
until the last minute! Get them into your mind soon after they are assigned, so
you have an opportunity to take a break (perhaps to ask questions) and come back to
the difficult problems
later.
When will problems be due? They
will usually be due on Tuesdays and Fridays (Mondays and
Fridays in weeks when there is a Tuesday exam). There
may be some exceptions due to exams, break, or problems that
are difficult enough to require more time.
How to submit? You will submit your homework solutions to
designated Moodle drop boxes. You can either compose your
solutions on
your computer or write them by hand and scan them to produce electronic copies. There are scanners in
F-217 and in the Logan Library (DRC). For each assignment, submit a
single file (can be a ZIP file); must be less than 5MB; aim for 2 MB or less.
There are no programming problems.
This is essentially an abstract mathematics course whose
area of application is computer science.
Due to limited time (yours and mine), I will only
require you to formally write up a subset
of the assigned problems. You should make sure you
understand all of them. But sometimes the time required to
write them clearly is greater than the time required to
understand/solve them, so I will not ask you to submit all
of them. My assistants and I will do our best to grade
all required problems, but occasionally we may have to grade
a proper subset of them.
The textbook has many exercises at the ends of the chapters; Almost all
are likely to be helpful; obviously I cannot assign all of them. For many of those
problems, reading and thinking about them will be instructive, even if you
don't have time to fully solve them. I recommend that you read them all,
regardless of whether they are assigned.
Get started early on all assignments! Sometimes you
will need some "incubation time" before the problem is due.
Policy on Late Assignments:
Because of the number of students taking this class and
because I am teaching an overload for the last half this term, I cannot
accept late assignments. Please submit whatever parts
you have done 8:15 AM on the due date. The Moodle drop
boxes will close shortly after that. In calculating
your assignment average, I will drop the score of the
assignment on which you
get the lowest percentage score, thus missing one assignment
or reading quiz
will not kill your grade.
Grade Components
| |
| 30% |
Assignments (including written homework,
quizzes, and any special assignments) |
| 70% |
Examinations (three in-class exams, 13%,
17%, 17%), and final exam, 23% |
In addition, in order to pass the course, you must have a passing score on
at least two of the five exams. The grading scale is a bit lower than in
other courses, to reflect the difficulty of some of the problems. It
is even possible that these numbers will be lowered a little bit, but you should not
count on it.
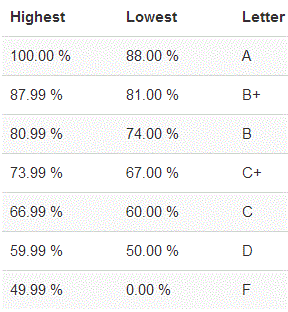
Grading scale for quizzes and homework problems. To
simplify the scoring process and let us focus on providing helpful feedback
instead of score nuances, the
possible point value for each quiz and each problem will be a multiple of 3, and will be
scored as that multiple times the following scale:|
3 Correct or a very minor error
2 Mostly correct
1 Some progress toward a solution
0 Nothing submitted, or nothing that demonstrates any understanding of the
problem.
Bounty for discovering new errata in textbook and
course materials.
If you are the first to find and report (in the bug_reports folder on
Piazza) an error in the textbook or in any document that I produce for the
course (including this syllabus), I will give you some bonus Assignments points.
The number of points is proportional to the importance and subtlety of the
error. Even spelling, punctuation, or grammar errors will count for something!
Already-known errors in the textbook:
http://www.cs.utexas.edu/~ear/cs341/automatabook/errata.html
Email, Discussion Forums, Classmates
I will communicate most announcements and assignment
clarification using Piazza. For messages
directly to individuals and for urgent announcements, I will use
Rose-Hulman email. You should check your email daily and make
sure that your mailbox does not fill up.
Sign up for the Piazza course at
piazza.com/rose-hulman/winter2014/macsse474. The
main course page on Piazza is
piazza.com/rose-hulman/winter2014/macsse474/home .
If you think that your question or comment
might be of general interest to people in
the class, please post it on one of the
course discussion forums on Piazza. First of
all, you may get an answer more quickly than
if you only send mail to me. Second, you may
get multiple people's perspectives. Third,
you will contribute to an active learning
community.
Other students in the course can often be
your best source of help. And they will also
learn more if they explain things to you.
Don't try to be the Lone Ranger in this
course, especially if you do not find the
course easy. If you have worked on
something for 30 minutes without making any
progress, it's probably time to seek help.
If you wait until the last grace day to
start working on a problem, there may not be
an opportunity for you to get help. My
goal is to respond to your email within 24
hours, and I will often respond much faster,
but you should not count on that during the
summer.
Anonymous Suggestion Box
I want your feedback on how the course is going and how it could be improved. While "nonymous" suggestions are even more useful than anonymous ones,
I'd like to know what you are thinking, even if you do not feel comfortable with letting me know who made the suggestion.
Thus the 474 Moodle site will contain an anonymous suggestion box. I will get your comments, but I
cannot trace who sends them.
All I ask is that you only use this only for serious suggestions, not to vent when you are momentarily frustrated.
You can also use this survey to tell me about things you like in the course and don't want to change. :)
If you ask a question in your
anonymous message, the only reasonable way I can reply is with a post to one of the course's discussion forums. I will do
that whenever I think my response is likely to be relevant to several students in the class.
Academic Integrity
Recall the Institute policy on academic misconduct:
“Rose-Hulman expects its students to be responsible adults and to behave at all times with honor and integrity.”
Exams and homework will be done on an individual basis except when explicitly noted. The simple rule of thumb for individual work is:
Never give or use someone else’s code or written answers.
Such exchanges are definitely cheating and not cooperation. The departmental statement on academic honesty has more detailed advice.
Unless I specify otherwise for some problem, you may communicate with other students about the problems, and work out solutions together.
But when you write it up to turn it in, you must do it on your own without reference to things that you wrote together,
to make sure that you have internalized it.
You should also acknowledge the collaboration in writing on your submission.
If you are ever in doubt about whether some specific situation violates this policy, the best approach is to discuss it with your instructor beforehand. This is a very serious matter that we do not take lightly. Nor should you.
You should never simply look at another student’s solution to get ideas of how to write your own. Beginning the process of producing your own solution with a copy of work done by other students
or found on the internet or in some fraternity file, etc., is never appropriate.
Plagiarism or cheating will, as a minimum penalty, result in a negative score (i.e., less than zero) for the assignment or exam. Egregious cases will result in a grade of “F” for the course. More importantly, such dishonesty steals your own self-esteem. So don’t cheat.
| |

