Homework 12 — Programming Language Paradigms

Objectives

Practice basic sequential programming in Erlang.

Due Date

Beginning of class session 31. (We don’t have class that day, because Curt is gone to OOPSLA. The due time is when class would have started.)

Tasks

1. Use your SVN client to update your ErlangHomework folder. Within the folder is a file sudoku.erl. All your work for this assignment must be done in that file.

2. The file sudoku.erl contains a partial implementation for a Sudoku puzzle solver. Your job is to complete the solver.

   Sudoku is a numeric puzzle game that originated in Japan. A Sudoku puzzle typically consists of an n×n matrix of n×n matrices. The solver’s task is to fill in each cell of the larger matrix with the numbers 1 through n². This must be done so that each row, each column, and each smaller matrix contains every number (and hence, no duplicates).

   The figure on the left below shows a starting configuration for a puzzle with n=3. The figure on the right shows the solved puzzle. Solutions are not necessarily unique, though in published puzzles the given configuration typically constrains the puzzle to a single solution.

   

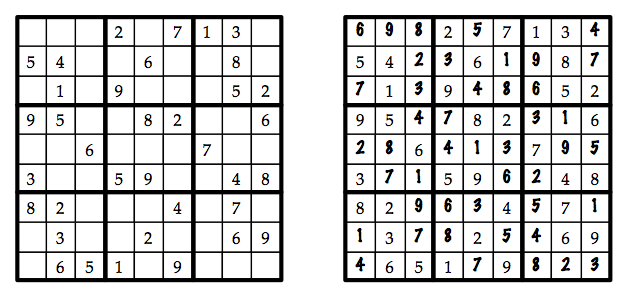
   Puzzle from Grand Master Su Doku Ultimate, by Wayne Gould, p. 11.

   Humans typically solve Sudoku puzzles by analyzing constraints and identifying cells where only one number fits, or pairs of cells where only two numbers fit. For example, consider where we could put a 1 in the top-center small matrix of the puzzle above—the one with 2, 7, 6, and 9 filled in. The 1 can’t go in the first row, because of the 1 in the top-right matrix. The 1 can’t go in the third row, because of the 1 in the top-left matrix. Finally, the 1 can’t go in the fourth column, because of the 1 in the bottom-center matrix. Thus, the 1 in the top-center matrix must go to the right of the 6.

   A computer program could use the same strategy, perhaps using dynamic programming. However, for small values of n, it is better to use a recursive search with backtracking.

3. Open sudoku.erl in your favorite text editor. Study the provided code. You will need to use some of the provided functions in your solution. In particular, you will probably be interested in:
   • is_valid/1
   • check_partial_solution/1
   • check_solution/1
   • test/0

4. You have two options for completing this assignment. You can follow the TODO items in the provided code, or you can create your own structure for the solution.

   • Option 1: Complete the TODO items in the provided code, creating additional helper methods if necessary.
   • Option 2: Replace the provided solve/1 function and the rest of the file with your own solution, writing any necessary helper methods. Your function must return a tuple {ok, Puzzle}, where Puzzle is a complete solution if one exists. If no solution exists, your solve function should return a tuple {impossible, Puzzle}, where Puzzle is the partial configuration for which no solution could be found.
5. Whichever option you choose, test your code by running sudoku:test(). Case 3 should report impossible; your program should solve the other cases.

Turn-in Instructions

Turn-in your work by committing it to your SVN repository.