(If it is hard to see, the two children of the root are red.) Insert the following nodes using the top-down insertion algorithm and show what happens (both rotations and re-colorings): 20, 10, 25, 27, 40. Please denote the red nodes very clearly, using red (best) or a key (acceptable). Work carefully - it will be hard to give partial credit if your answer is incorrect.
(10 points) Let maxNNDepth(T) and minNNDepth(T) denote the number of (non-NULL) nodes on the longest and shortest (respectively) paths from the root to a NULL_NODE in tree T. Note that maxNNDepth(T) = 1 + h(T), where h(T) is the height.
- (6 points) Explain why maxNNDepth(T) ≤ 2*minNNDepth(T) for any red-black tree T, using properties of red-black trees.
- (0 points) Nothing to do, just an observation: it can be shown that maxNNDepth(T) ≤ 2*minNNDepth(T) for any height-balanced (AVL) tree T, as well. [If you're curious and have time, you might try proving this by induction over the height. NO bonus points for this, just for fun. Suggestion: you might find it easier to prove that h(T) ≤ 2*minNNDepth(T) - 1. Also, in the general case, you may "assume without loss of generality" that (say) h(TL) ≤ h(TR).]
- (4 points) What can we conclude about the asymptotic best-case running time of an unsuccessful search on either type of tree?
As a larger example, this tree was built from the strings, "ARGEDFKJHWS" and "R22200LL0L0":
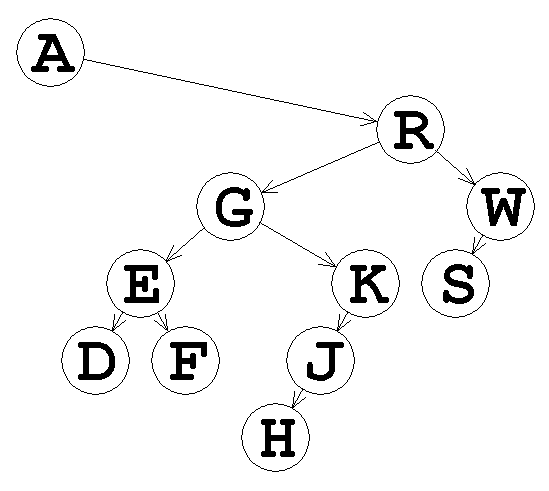
This format should sound familiar - see HW3 and its solution for more details. Note that this can construct any binary tree of characters, not just BSTs. I am posting two hints here, but I strongly suggest that you try to develop an algorithm first before referring to them.