(10 points) Exercise 19.2 included finding the probability (based on equally likely insertion orders of each of the 24 permutations) of each of the 14 different trees that can result when inserting the numbers 1, 2, 3, and 4 into an initially empty BST (with no re-balancing).
- With the same assumption (that all permutations of the four numbers are equally likely), what is the (weighted) average height of the BSTs?
- With the same assumptions, do the same exercise for inserting the four numbers into an AVL tree. In other words, what is the average height of the AVL trees?
(If it is hard to see, the two children of the root are red.) Insert the following nodes using the top-down insertion algorithm and show what happens (both rotations and re-colorings): 20, 10, 25, 27, 40. Please denote the red nodes very clearly, using red (best) or a key (acceptable). Work carefully - it will be hard to give partial credit if your answer is incorrect.
As a larger example, this tree was built from the strings, "ARGEDFKJHWS" and "R22200LL0L0":
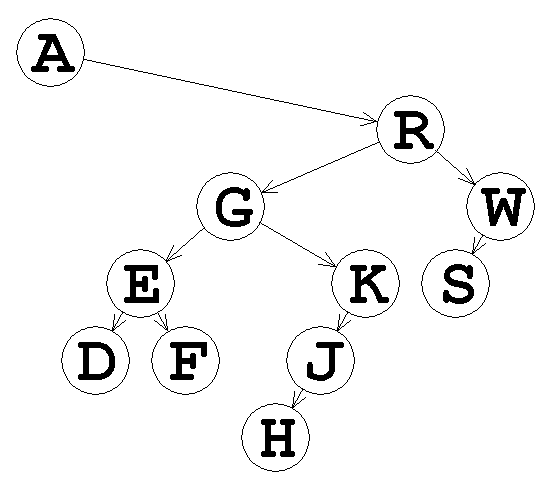
This format should sound familiar - see HW3 and its solution for more details. Note that this can construct any binary tree of characters, not just BSTs. I am posting two hints here, but I strongly suggest that you try to develop an algorithm first before referring to them.