CSSE 230
Data Structures and Algorithm Analysis

Homework 4 - 40 points

To Be Turned In

1. (20 points) Calculate the exact average-case time complexity of the binary search algorithm shown in Weiss, Figure 5.11. Only consider successful searches (where the item we are looking for is actually in the array) and assume all elements are equally likely to be the one we are searching for. 

1. Complete this for N=7 elements in the array.
2. Complete this for N=15 elements in the array.
3. Complete this for N = 2^k - 1 for some integer k ≥ 0, generalizing from what you found in (a) . 

Hint: For each i, count how many of the array elements will be found after binary search examines exactly i array elements. (For example, the middle element is the only one to be found after examining one array element, and there are two elements that can be found after examining two array elements.) Then sum over all and divide to find the average. For the generalization, you'll use a summation. You need to convince me somehow that your summation is correct, perhaps using a table or words. Once you have done that, then you may find the following formula useful: 

 

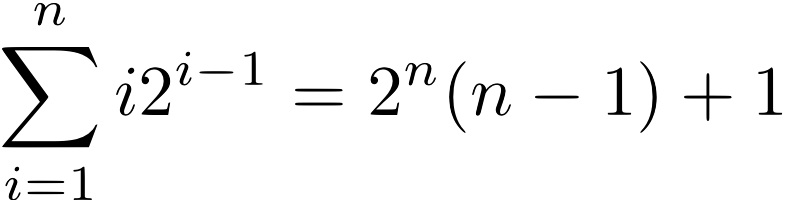
After you have done that, you'll get a messy expression with lots of terms in it. Take the limit as n gets large so some terms go to zero. You'll end up with a much simpler expression that should be clearly between 1 and log (n), like we said in class.

(Hint: Weiss 5.6.2 about binary search gives the big-oh answer for this problem. You probably won't get the same answer as him for the exact case, but you can use his big-oh answer to help check your work.)

2. (20 points) Checkout the TreePractice project from your SVN repository. Complete them, per the given specifications, and commit your solutions back to the repositories. These are good practice for exams. Recall the recursive pattern from day 7. Strategy as the recursive problems get more complicated: on some problems, you will want to communicate information down the tree as you recurse, so you will find it helpful to add a parameter to your recursive method. You may also use objects as return values to return multiple things up the tree.

For Your Consideration

These problems are for you to think about and convince yourself that you could do them. It would be good practice to actually do them, but you are not required to turn them in.

• public static void main(String[] args) {
   Collection<Collection<String>> a = new ArrayList<Collection<String>>();
   String[][] arrays = {{"abc", "def", "ghi"}, 
   {"xyz", "uvw", "abc", "abc"}, 
   {"a", "ab", "abc", "xyz", "abc"}};
   for (String[] sArray : arrays){
   Collection<String> a1 = new ArrayList<String>();
   for (String s: sArray)
   a1.add(s);
   a.add(a1);
   }
   System.out.println(count(a, "abc"));
  } 
  

• Other good problems to think about: 15.1[15.1], 15.3[15.3], 15.5[15.5], 15.9[15.9], 15.10[15.10], 15.12[15.12], 15.13[15.13], 17.3[17.3], 17.4[17.4], 17.5[17.5], 17.6[17.6] , 17.16[17.16]