CSSE 230
Data Structures and Algorithm Analysis

Homework 1  - 53 points

To Be Turned In (at the end of this document are some problems to consider but not turn in)

These are to submitted to the Homework 1 Drop Box on Moodle as a single file in either MSWord or pdf format. You can write your solutions out by hand and scan them (there is a networked scanner in F-217, and several scanners in the library's Digital Resource Center), or create a file on your computer directly. Some apps also allow you to take a photo with your phone or tablet and save it as a pdf. After you have submitted, click on the drop box again to verify that your submission was successful.

 

These homeworks used to be called "written assignments", but that was a slight misnomer, because occasionally these assignments include small programming exercises.

Some homeworks will contain problems that are very challenging.  You should read them as soon as they are assigned. Then if you need a couple of days to ponder one of them, you will have them.

The numbers in [square brackets] are problem numbers from the third edition of Weiss, for those who have that version.

Late days may be used or earned for homeworks.

In problems #2,3, and 4, if you don't know what Big-Theta running time is, you will be safe giving Big-Oh. 

  1. (5 points) Weiss exercise 2.13 [2.11]. Hint: If one calls resize(ar) from main(), ar is unchanged. Why? Drawing a box-and-pointer diagram may help you.
  2. (6 points) Choose one of the following answers for each part: Θ(log (N)), Θ(N), Θ(N log (N)), Θ(N2), or Θ(N3). What is the Big-Theta running time of ...
    1. ...an unsuccessful sequential search of an unordered array that contains N elements?
    2. ...an unsuccessful binary search of an ordered array that contains N elements?
    3. ...a merge sort of an array that contains N elements?

  3. (10 points) For each of the following four code fragments, similar to Weiss problem 5.20, first write the exact number of times the "sum++" statement executes in terms of n, using the ceiling or floor if needed. (Hint: two of them do.) Then use that to also write the Big-Theta running time.  
    1. for (int i = 0; i < n; i++) 
         sum++;
       
    2. for (int i = 0; i < n; i += 2) 
         sum++;
       
    3. for (int i = 0; i < n; i++) 
         for (int j = 0; j < n; j++) 
            sum++;
       
    4. for (int i = 0; i < n; i++) 
         sum++;
      for (int j = 0; j < n; j++) 
         sum++;
       
    5. for (int i = 1; i < n; i *= 2) 
         sum++;
  4. (3 points) Weiss exercise 5.11 [5.8]. Give the exact running time in terms of N, the big-Theta running time, and a brief explanation of the exact running time.
  5. (4 points) In asymptotic analysis, it's very useful to know if the base of a logarithm mattters. We'll consider two functions, log2(n) and log10(n). Is it true that log2(n) is θ(log10(n))? I suggest that you graph them first to get a feel for it. Then calculate the ratio log2(n)/log10(n) for n=1000. Then repeat for the ratio  log2(n)/log10(n) for n=1,000,000. What do you notice? Why is this true? (Hint: you can use the change of base formula for logarithms.) Submit all your calculations and explanations, except for the graph. [Extra, not for credit: if it is true that log2(n) is θ(log10(n)), is it also true that 10n is θ(2n)?]    
  6. (5 points) When the input size is N, algorithm A uses 5 N log N operations, while algorithm B uses N2 operations. For small values of N, algorithm B is faster; for large values of N, algorithm A is faster. Determine the smallest possible integer N0 such that for all N > N0 algorithm A is faster than algorithm B. Explain how you know that this is the correct integer. (Hint: if solving for N isn't working for you, graphing this in Maple and submitting your graph sounds like a great idea!)
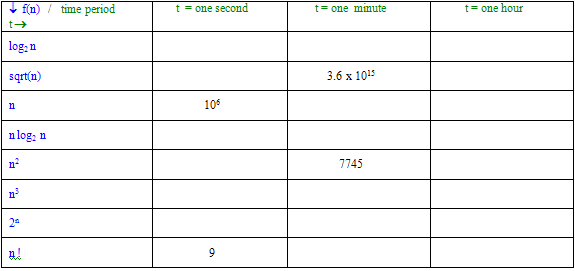
  7. (20 points) For each function in the following table, determine the largest size n of a problem that can be solved in time t, assuming that the problem takes f(n) microseconds, where f(n) is the function in the left column.  Throughout this course, unless I specify otherwise, log n means the logarithm in base 2 of n.    If the answer is small, give the exact answer. (Note if you would get a non-integer result, your answer must be the floor of it - make sure you understand why.)  If it is a million or larger, you can use scientific notation, with a couple of decimal places of precision. Hint: Maple is your friend! If it overflows Maple (like line 1 might), you may give an expression instead. 

For Your Consideration

These problems are for you to think about and convince yourself that you could do them. It would be good practice to actually do them in the next couple of weeks, but you are not required to turn them in.