CSSE 230
Data Structures and Algorithm Analysis
Homework 9 - 50 points
To Be Turned In
Submit to the drop box.
- (10 points) Weiss Exercise 8.9. This should be fairly easy
if you followed the derivation of the quicksort average case runtime
that we did in class.
- (10 points) Weiss Exercise 8.14[8.14]. You don't need
exact Java code, but explain your algorithm in enough detail to
convince us it works in O(Log N) time. This will require some insight -
don't leave it to the last minute!
- (10 points) Weiss Exercise 19.8 (ignore the "with proof"
part). (We hope this looks familiar to you - do you recall which
EditorTrees JUnit test this was?)
- (20 points) In this problem,
we consider completely full binary trees with N nodes and height H
(so that N = 2H+1 – 1 )
(a) (5 points) Show that the sum of the heights of all of the nodes of
such a tree can be expressed as
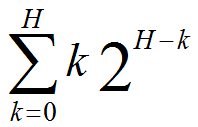
(b) (15 points) Prove by induction on H that the above sum of the
heights of the nodes is N - H - 1.
You may base your proof on the summation from part (a)
(so you don't need to refer to trees at all), or
you may do our "standard" binary tree induction based on
the subtrees (using the definition that a non-empty binary tree has a
root plus left and right subtrees). We find the tree approach more
straightforward, but you may use the summation if you prefer.
For Your Consideration
These problems are for you to think about and convince
yourself that you could do them. It would be good practice to actually
do them, but you are not required to turn them in.
- Weiss exercise 6.4 [6.4].