CSSE 230
Data Structures and Algorithm Analysis

Homework 6  -  42 points

Don't forget that you should be making notes about your team and team members, for eventual use in the EditorTrees team evaluation.

To Be Turned In

Questions 1 and 2 should be submitted to the drop box and the last two questions should be committed to your repository in SVN.  You may earn a late day by submitting all parts early, or use a late day if submit any part late.

    1. (12 points) Fill in the following table. Be very careful to get the exact values. Most of the credit will be for the last column. Don't use the AVL approximation formula (H < 1.44log(...)). Instead, draw trees and look for the patterns, like we did on day 13 in class.

      Feel free to include explanations of your answers. correct_answer → full_credit.  wrong_answer + no_explanation → no_credit.

      1/2 point for each entry in the first two columns, and 2 points each for each entry in the last column.

      n Height of shortest binary tree with n nodes Height of tallest binary tree with n nodes Height of tallest AVL tree with n nodes
      7 2 6 3
      8      
      370      
      17000      
      50000      

    2. (10 points) Exercise 19.2 included finding the probability (based on equally likely insertion orders of each of the 24 permutations) of each of the 14 different trees that can result when inserting the numbers 1, 2, 3, and 4 into an initially empty BST (with no re-balancing).

      1. With the same assumption (that all permutations of the four numbers are equally likely), what is the (weighted) average height of the BSTs?
      2. With the same assumptions, do the same exercise for inserting the four numbers into an AVL tree. In other words, what is the average height of the AVL trees?
    3. (20 points) Checkout the PreorderBuildTree project from your SVN repository. In this problem, you'll create another Binary Tree constructor, one that constructs a Tree with Character data from two pre-order lists: a string of data and a string of children. For example, t = BinaryTree("abc", "200") would create a full tree of height 1 with root = a and two children b and c, and t = BinaryTree("cbad", "2L00") would create the minimum height-balanced tree of height 2, with an in-order traversal of "abcd".

      As a larger example, this tree was built from the strings, "ARGEDFKJHWS" and "R22200LL0L0":

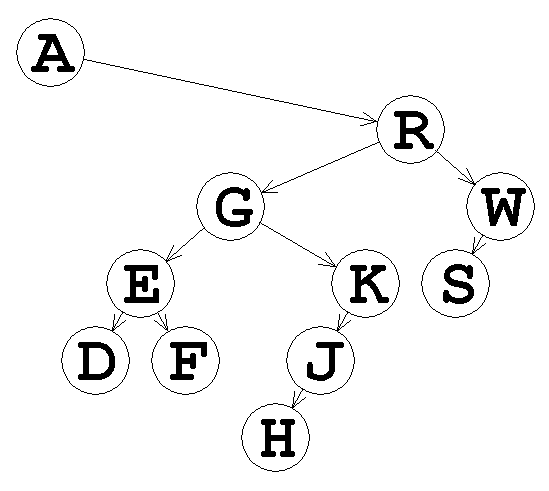
      This format should sound familiar - see HW3 and its solution for more details. Note that this can construct any binary tree of characters, not just BSTs. I am posting two hints here, but I strongly suggest that you try to develop an algorithm first before referring to them.

    Other problems for your consideration

    6.31[6.17], 6.37[6.22], 7.3[7.3], 7.4[7.4], 7.23[7.19], 7.29