CSSE413 Artificial Intelligence

Fall 2006-2007

Programming Assignment -- Search

(Please put in your turnin folder, labeled as HW3)

Due as described on the assignment webpage

Intro Discussion

Goal:� The goal of this lab assignment is for you to gain expertise in using intelligent search in a domain well suited to it. �Specifically, the problem is to create an A* search for a variation of the domain called �blocks world,� so that you can find guaranteed optimal solutions, and also so that you can find suboptimal solutions fast.� Both of these are common roles for search.

Domain:� The basic domain �blocks world� is a famous one in AI, often used as a model domain for planning.� We�ll get back to talking about it for that purpose in Ch. 11, for example.� Let�s first describe the �ordinary� version of it, like that used in Ch.11.� In blocks world, you are presented with a set of stacked blocks on a table, which must be rearranged into some other stacks, using a single mechanical arm, as pictured in Fig. 1:

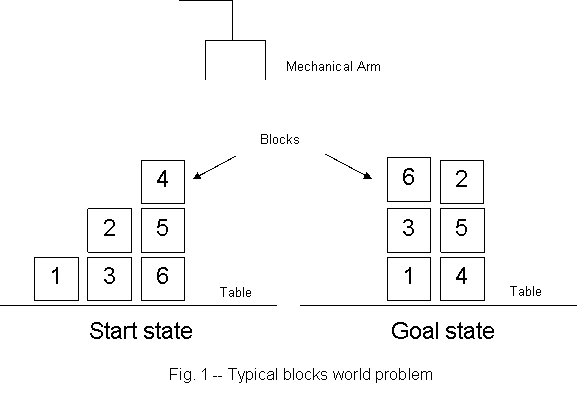
The problems are always shown with two arrangements of the same blocks on a table, one called the Start State and the other the Goal State!� Assume you are actually given the blocks in the Start State, and what you need to do is move them into the Goal State.� There is a single, magical, mechanical arm which can lift up the blocks and move them, one at a time. Each block starts and ends either on the table or else exactly on top of another block.� In making progress on the problem, you will go through a sequence of other states, trying to convert the Start State to the Goal State.� An �optimal� solution to a blocks world problem takes you through the minimal number of such intermediate states.� The blocks given in each state are of course always the same, as shown in the Start State and Goal State in Fig 1.

For simplicity, assume that all moves from one state to the next can be described in the following rather concise way to the magical, Mechanical Arm which performs them:

Move(block_ID, start_position, end_position),

Where the block ID is one of those pictured in the problem, and the positions are either �On Table� or �On � some other block.� For example, a legal move from the Start State would be:

Move(4, On 5, On Table),

Legalities in the domain:� It is not legal to move blocks out from under other blocks, or to insert a block into the middle of a stack.� The Table is assumed to be infinite in size, allowing any number of stacks in the Start State, Goal State, or any intermediate state.� All blocks are the same square shape and, traditionally, only two-dimensional problems are given, like the one shown.� You might be wondering if �Block 1� is really in the same place in the Start State and Goal State shown in Fig. 1; just to be perverse, let�s say �Yes,� meaning that the block positions are really relative, and a solution is valid even if the first stack ends up being in a different place on the table.� To make things easy, let�s say it would still be considered a valid Goal State if the two stacks shown in the Goal State of Fig. 1 were reversed.

Your variation of this domain:� This is called �colored blocks world,� and it makes the following slight complication to the traditional blocks world:� There can be more than one block with the same identity!� This is shown as having multiple blocks of the same colors, in Fig. 2:

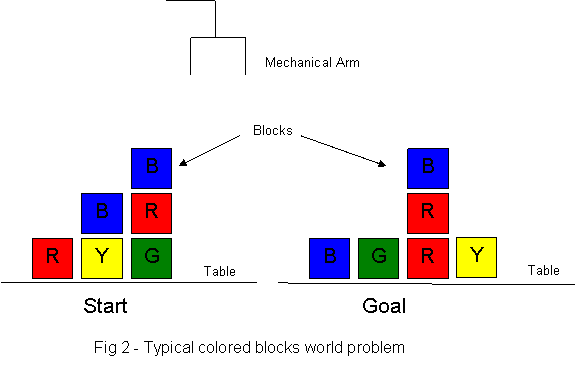
Thus either blue (�B�) block in the Start State could play the role of either blue block in the Goal State, just to give an example.� An optimal solution again would transition the Start State to the Goal State in a minimal number of moves through intermediate states.� However, in colored blocks world this might be achieved in more than one way!

Hint: To describe transitions using the mechanical arm in this domain, you need to give the blocks unique identities, so that you can say uniquely what is being moved to get from one state to the next.

Your project: �Use A* search to solve problems in colored blocks world!� Specifically, it should do the following things:

1. �Read in files containing problem descriptions such as this one for the problem shown in Fig. 2 (you can vary the format of these problem descriptions to suit your language):

(Start

(On Table Red-1)

(On Table Yellow-1)

(On Yellow-1 Blue-1)

(On Table Green-1)

(On Green-1 Red-2)

(On Red-2 Blue-2))

(Goal

(On Table Blue-x1)

(On Table Green-x2)

(On Table Red-x3)

(On Red-x3 Red-x4)

(On Red-x4 Blue-x5)

(On Table Yellow-x6))

2. �Display the solutions as a series of moves, as described, which take the Start State through a series of intermediate states to the Goal State.� For example, we could solve the problem in Fig. 2 with these moves:

Move(Blue-1, On Yellow-1, On Table)

Move(Blue-2, On Red-2, On Table)

Move(Red-2, On Green-1, On Red-1)

Move(Blue-2, On Table, On Red-2)

at which point the Goal State has been achieved, if as specified we allow the convention that any Red block can play any role of a Red block in the solution, and similarly for the other colors.

3. �Use an admissible heuristic of your invention to solve these problems optimally.

4. �Allow a way to �tune� that heuristic so as to improve its performance on large problems, at possibly a slight additional cost in the length of the solution path.� Note that there is an easy solution to all these problems, namely, just unstack all the blocks from the Start State, and then restack them in the right order for the Goal State.� So, a slightly less than optimal solution found by your algorithm should, in general, be more efficient than that!

Tools:� You will have two development environments to choose from; you can pick which one is right -- for you -- for this task.�� Namely, you can use either Scheme or Java.� So long as your assistants and instructors can read your source code and test your programs in either Petit Scheme or Eclipse, respectively.

You may want to spend a little time designing how you want your solution to be put together. Since it is to read in and solve problems of arbitrary size, some forethought on that will help in the long run.

You�ll want to decide what a �node� will look like, in general, and a �state� of each kind of problem at that node, and how you might need to remember �paths� so you can report what a �solution� looks like after a successful search.� And how to parse the list of �open nodes� with this particular search method.

Additionally, consider exactly how you want the problems to be described, as input to your programs, to minimize the effort for that. �Something like the method shown above probably works better in Scheme, not so well in Java.� Your instructor will be open to alternative ideas on this, so long as it�s feasible for him to test your program!

Note: It would be useful to take a crack at this early � If it turns out to be too much, We�ll revise the assignment downward or extend the deadline. However, this is about the right size for you to end-up feeling like you really designed software with some general search capability.

This is an individual assignment, not a team assignment.

Detailed description

1. Be sure you understand how A* works, from Ch 4 in Russell & Norvig.

1a.� If you want to �warm up� with an unintelligent search from Ch 3, that�s fine.� If it really runs, you can include that in what you turn in for some small amount of extra credit.� However, mostly we�re interested in how well you can use intelligent search (A* in particular).

2. Be sure you understand how colored blocks world is defined, from the above definition.� Ask questions early!

3. If you need help, ask for it, and we or the assistants will make sure you get plenty!

4. When you turn in the assignment --

� Make it obviously HW3 in your turnin folder, etc.

� Include a readme.txt file that makes it clear how to run it � with sample data structures, directions on how to �tune� it for non-optimal faster search, etc.

� Include some sample test results, so that I know you think your program works, and so that we can replicate those tests, at least.

� And if you know any limits, like "Don't try more than 10 blocks or it blows up on my PC," let me know.