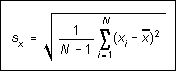Summary of Error Analysis Formulas

1. The standard deviation of a quantity x, estimated from N identical trials x₁, x₂, x₃, . . ., x_N of an experiment, is given by

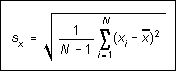(2)

2. The standard deviation estimates how well a typical single measurement of x is likely to estimate the "true" value. The standard deviation of the mean value of N trials is called the standard error of the data set. It estimates how precisely the mean of the N trials is likely to estimate the mean value. For N trials, the standard error is

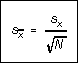(3)

3. Propagation of errors: If you have measured x and want to calculate some other quantity Q from it, then, if the errors are not too large,

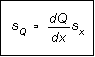(7)

If several independent measured variables x, y, z, . . . all contribute to the calculated quantity Q, their error contributions are added in quadrature:

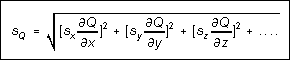(9)

Special Cases

For a sum where a, b, c, . . are constants,

(11)

For a product of powers where A, m, n, etc. are constants,

(13)

where is the fractional standard error in x, etc. This is easily the most useful of all the special-case formulas.

For a logarithmic dependence ,

(8c)