Chapter 6: Other Experiments
Fluid Friction
References
Crummett and Western, Physics: Models and Applications,
Sec. 16-6,7
Halliday, Resnick, and Walker, Fundamentals of Physics (5th
edition), Sec. 15-8
Tipler, Physics for Scientists and Engineers (3rd edition),
Sec. 11-4,7
Introduction
The frictional or "viscous" drag force on an object moving
through a fluid depends, among other things, on the object's size. In this
experiment, you will investigate the form of the dependence, and measure
the "viscosity" of a particular fluid.
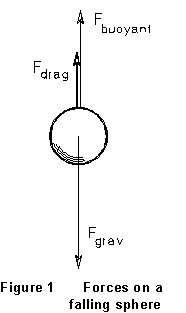 Consider a sphere
of radius R, moving at velocity v through some fluid. A drag
force FDrag acts on it, due to internal friction in the
fluid that it has to shove out of the way. If the speed of the motion is
not too great, the flow of the fluid around the sphere will be "laminar"
or non-turbulent in nature. Under these conditions, the drag force is directly
proportional to the velocity, and depends in some simple (but unspecified)
way on the radius of the sphere. As a trial form, suppose that
Consider a sphere
of radius R, moving at velocity v through some fluid. A drag
force FDrag acts on it, due to internal friction in the
fluid that it has to shove out of the way. If the speed of the motion is
not too great, the flow of the fluid around the sphere will be "laminar"
or non-turbulent in nature. Under these conditions, the drag force is directly
proportional to the velocity, and depends in some simple (but unspecified)
way on the radius of the sphere. As a trial form, suppose that
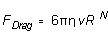 (1)
(1)
where N is an integer to be determined experimentally, and the
constant 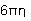 is a characteristic
of the particular fluid. (
is a characteristic
of the particular fluid. (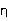 is called the viscosity of the fluid. In the old "cgs"
system, viscosity is measured in poises, after Poiseuille; exactly
what a poise is, of course, depends on what N turns out to be.)
is called the viscosity of the fluid. In the old "cgs"
system, viscosity is measured in poises, after Poiseuille; exactly
what a poise is, of course, depends on what N turns out to be.)
When the sphere falls freely through the fluid, there are three forces
acting on it: the pull of gravity (its weight), the buoyant force of the
fluid, and the viscous drag force given by (1). As the falling sphere accelerates,
the drag force Fdrag increases until the resultant force
on the sphere is zero; thereafter, in equilibrium, it will fall at a constant
("terminal") velocity. Under these conditions,
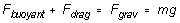 (2)
(2)
Now if the density of the sphere is 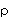 ,
and that of the fluid is
,
and that of the fluid is 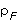 ,
then
,
then
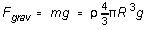
and 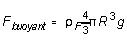
since, by Archimedes' principle, the buoyant force FB
is equal to the weight of the displaced fluid. Substituting these into
(1) and (2) and solving for v gives
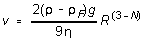 (3)
(3)
That is, the dependence of v on R in a given fluid will
be a simple power law. Thus if we graph ln(v) vs. ln(R),
we ought to get a straight-line graph with slope (3-N) and an intercept
given by 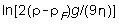 . In this
experiment, you will determine the integer N -- that is, the specific
form of Equation (1) -- by this means.
. In this
experiment, you will determine the integer N -- that is, the specific
form of Equation (1) -- by this means.
Carrying out the experiment is complicated slightly by the fact that
the sample of fluid in which you must work is of limited size. Equation
(1) contains no reference to the fluid except the intrinsic properties
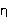 and
and 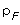 ,
so it must refer to an infinite body of the fluid. In reality, internal
friction makes a connection between the motion of the falling sphere and
the walls bounding the fluid in which it moves. As a result, the velocity
of fall is reduced somewhat, compared to that of the same object falling
in an endless body of the fluid. Experiment has shown that this reduces
the velocity by a factor K given by
,
so it must refer to an infinite body of the fluid. In reality, internal
friction makes a connection between the motion of the falling sphere and
the walls bounding the fluid in which it moves. As a result, the velocity
of fall is reduced somewhat, compared to that of the same object falling
in an endless body of the fluid. Experiment has shown that this reduces
the velocity by a factor K given by
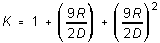 (4)
(4)
where R, as above, is the radius of the falling sphere, and D
the diameter of the cylindrical tube in which it is falling.
Equipment
- fall tubes (3 sizes) with steel and Teflon spheres
- electronic timer
- meter stick
- micrometer calipers
Procedure
In the experiment, the spheres are steel 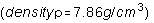 ball bearings and Teflon
ball bearings and Teflon 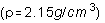 balls sealed into cylindrical plastic pipes filled with Dow-Corning 200
fluid
balls sealed into cylindrical plastic pipes filled with Dow-Corning 200
fluid 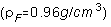 . Tubes
of three different sizes are provided. Each of the short tubes contains
a #2 and a #3 size steel ball; each medium length tube contains a #4 and
a #5 size ball. Each long narrow pipe contains either a #3 or a #4 steel
ball (the pipes are marked) and a Teflon ball. The diameters of the steel
balls are:
. Tubes
of three different sizes are provided. Each of the short tubes contains
a #2 and a #3 size steel ball; each medium length tube contains a #4 and
a #5 size ball. Each long narrow pipe contains either a #3 or a #4 steel
ball (the pipes are marked) and a Teflon ball. The diameters of the steel
balls are:
#2: 1.59 mm
#3: 2.38 mm
#4: 3.18 mm
#5: 3.97 mm
Consider these to be known exactly.
(1) Measure the time required for one of the spheres to fall
a measured distance (reference lines are scribed on the tube walls). Repeat
the measurement several times to obtain an average. Try to manipulate the
tube each time so that the sphere you're watching is falling along the
central tube axis, while the other sphere in the tube is falling near the
wall. Repeat the measurements on the other sphere in the same tube.
(2) Exchange fall tubes with other experimenters and repeat the
measurements of step (1) on the other two tube sizes. Altogether you should
acquire data on five different steel-ball-and-tube-geometry combinations,
and one Teflon ball, in three tubes.
(3) Use a meter stick to measure the distance between the reference
lines on the wall of each tube you used, and the tubes' inside diameters.
Use micrometer calipers to measure the diameters of the steel spheres.
Analysis
(1) For each configuration of a steel ball and tube geometry,
calculate the average terminal velocity and its standard error. Be sure
to account for the uncertainty in both the distance and time of the falling
sphere. Multiply each by K from Equation (4) to "correct"
the velocity to what it would be if the sphere were falling in an infinite
medium. Make a table showing 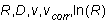 ,
and
,
and 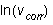 for the five
steel balls.
for the five
steel balls.
(2) Make a graph of 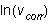 vs.
vs. 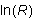 ; according
to Equation (3), it should be a straight line. Find the slope and the intercept
of the best straight line through all the data, with error estimates. The
slope of the graph should be 3 - N. Given that N
is a positive integer, what must be its value? Write Equation (1) using
the appropriate value for N; this is a fundamental law of fluid
friction for the case of laminar (non-turbulent) flow.
; according
to Equation (3), it should be a straight line. Find the slope and the intercept
of the best straight line through all the data, with error estimates. The
slope of the graph should be 3 - N. Given that N
is a positive integer, what must be its value? Write Equation (1) using
the appropriate value for N; this is a fundamental law of fluid
friction for the case of laminar (non-turbulent) flow.
(3) From Equation (3), using the value you have found for
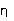 , calculate
a value of the viscosity for each of your five steel ball trials. Determine
the mean value and the standard error of the mean from your values. Given
the form you found for Equation (1), what must be the dimensions
of viscosity? What is its SI unit? How is this unit related to the
poise? Report your final value for
, calculate
a value of the viscosity for each of your five steel ball trials. Determine
the mean value and the standard error of the mean from your values. Given
the form you found for Equation (1), what must be the dimensions
of viscosity? What is its SI unit? How is this unit related to the
poise? Report your final value for 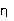 ,
with error, in SI units.
,
with error, in SI units.
(4) For your data on the Teflon ball in the long fall
tube, calculate the mean terminal velocity and its standard error. Use
Equation (3) with appropriate value for N, and Equation (4), to
infer the radius of the Teflon sphere. (Don't forget to account for the
correction factor K!) Estimate the error in your result from the
uncertainties in v and in 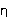 .
.
Results
Your results to be reported are: the specific form of equation (1) (called
Stokes' law), the value of the viscosity of Dow-Corning 200 fluid (with
uncertainty), and the value of the radius of the Teflon sphere (with uncertainty).
Your analysis plainly assumed that the spheres were falling, over the
distance for which you timed them, at a constant velocity. The distance
through which the object falls, starting from rest, while coming to
its constant terminal speed, is on the order of v2/g.
Estimate this distance; is the assumption justified in all the cases you
measured?
Chapter 6 -- Other Experiments -- Specific
Heat Capacity
last update 7/97
 Consider a sphere
of radius R, moving at velocity v through some fluid. A drag
force FDrag acts on it, due to internal friction in the
fluid that it has to shove out of the way. If the speed of the motion is
not too great, the flow of the fluid around the sphere will be "laminar"
or non-turbulent in nature. Under these conditions, the drag force is directly
proportional to the velocity, and depends in some simple (but unspecified)
way on the radius of the sphere. As a trial form, suppose that
Consider a sphere
of radius R, moving at velocity v through some fluid. A drag
force FDrag acts on it, due to internal friction in the
fluid that it has to shove out of the way. If the speed of the motion is
not too great, the flow of the fluid around the sphere will be "laminar"
or non-turbulent in nature. Under these conditions, the drag force is directly
proportional to the velocity, and depends in some simple (but unspecified)
way on the radius of the sphere. As a trial form, suppose that