Table of Contents

Chapter 5: Waves Experiments

Resonances in Strings

References

Crummett and Western, Physics: Models and Applications, Sec. 15-2,5
Halliday, Resnick, and Walker, Fundamentals of Physics (5th ed.), Sec. 17-3 to 6
Tipler, Physics for Scientists and Engineers (3rd ed.), Sec. 13-6

Introduction

Any mechanical system has certain characteristic modes of vibration, each mode with a particular characteristic frequency. If the system is made to vibrate by driving it with an external source, it will respond strongly only when the source frequency is equal to, or near, one of these characteristic frequencies. This phenomenon is known as resonance. The characteristic resonance frequencies of a one-dimensional vibrating system are in simple whole-number ratios; they form what is known as a harmonic series. In this experiment, you will observe and measure the harmonic frequencies of a simple one-dimensional system: a stretched string. (It's interesting to note that a large number of musical instruments are based on this system.)

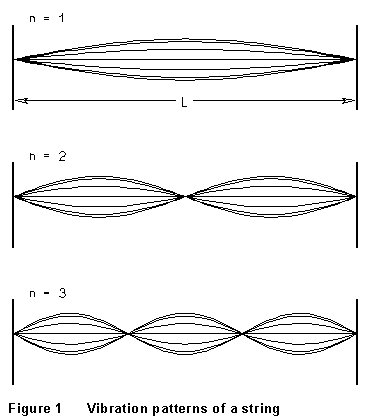
If a string is stretched between fixed end points, large-amplitude vibrations of the string can only occur with a frequency such that a whole number of half wavelengths will fit between the ends. The possible vibration patterns are therefore like those sketched in Figure 1, and the corresponding frequencies are given by

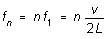for n = 1, 2, 3, . . . (1)

where

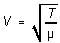(2)

is the speed of traveling waves on the string. In (2), T is the tension in the string and µ its mass per unit length.

The experimental arrangement is sketched in Figure 2. The resonating system is driven by a loudspeaker connected to a variable-frequency oscillator, so that the driving frequency can be varied at will. For the vibrating string, your eye is all the "resonance detector" you need. The pulley-and-weight arrangement in Fig. 2 allows one to vary the tension in the string.

Equipment

A NOTE ON THE APPARATUS: The HP 5314A Frequency counter-timers will give either frequency (cycles/sec or Hz) or period (sec) information, averaging over 1, 10, or 100 samples of the input signal. They read unpredictably if the input signal is too big, but this can be fixed by pushing the X20 attenuator button. At high frequencies (106 Hz or more), the period readings become inaccurate; below about 100 Hz, the frequency readings are inaccurate. If the "overflow" light comes on, it indicates that one or more of the most significant digits are being lost from the display; try another setting. On the Wavetek signal generators, make sure the "frequency sweep" and "DC offset" features are turned off; you want a steady signal frequency.

Procedure A. Stretched String

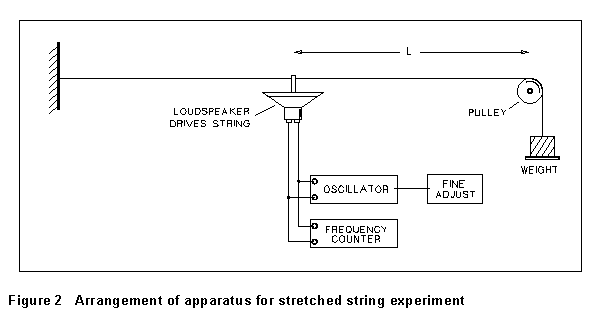
(1) Fasten one end of a string to the support and run the string over the pulley at the other end. Fasten a weight hanger to the free end of the string as in Figure 2. You may want to add some extra weight to the hanger to increase the total mass, which determines the tension in the string; consult your instructor. Connect the HI output of the oscillator to the loudspeaker and the LO output to the A input of the HP frequency counter. Connect the frequency fine-adjust box to the VCG input of the oscillator.

(2) Pass the string through the slot cut in the small rod that extends from the speaker cone. Measure the length of string from the speaker rod to the point at which the string touches the pulley. Repeat this measurement several times.

(3) Turn on the oscillator and, starting at a frequency around 10 Hz, increase its frequency slowly until the section of string between the loudspeaker and the pulley is vibrating in its fundamental mode (as in Fig. 1a) with maximum amplitude. The fine-control box may help you get precisely on the resonance frequency. (It increments the oscillator frequency by an amount up to about .08 of the FREQ MULT control.) NOTE: here and in the next two steps, you should use as low an oscillator signal amplitude as you can, and still locate the resonance frequency clearly.) Record the oscillator period as read by the HP-5314A. (This will be more accurate than recording the frequency reading. See the note above.)

(4) Turn the oscillator frequency up until the string vibrates in its second mode, and record the oscillator period. Continue in this way until you have measured as many of the modes as you can clearly discern. You should be able to measure at least through f4. (You will probably have to increase the driving signal amplitude as you go to the higher frequencies.)

(5) Exchange roles with your lab partner and repeat steps (3) and (4), so that you have two independent determinations of each resonance frequency.

(6) Your lab instructor will supply you with some appropriate pre-measured lengths of the same string. Weigh these on the chain balance, and calculate the mass per unit length of the string (µ), with error estimate. (Note: In doing this, you won't have to add any weights to the balance pan. The slider and chain provide enough weight to measure a meter or so of string.)

Analysis

(1) Tabulate your observed values of the resonance frequencies of the string. For each mode of vibration, show the individual determinations of fn, their average value, and the corresponding value of f1 = fn/n. Find the mean and standard error of the values of fn. Are your data consistent with the expected behavior fn = nf1, within experimental error?

(2) Use your overall mean value of f1 in Equation (1) to find the wave velocity on the string, and find the error in this determination. Calculate the expected value of v from Equation (2), and find the error in this determination. Are your expected and observed values of v consistent with each other?

Chapter 5 -- Waves Experiments -- Prism Spectrometer -- Dispersion Curve for Glass (Version 1)

last update 7/97