Chapter 4: Electricity and Magnetism Experiments
Magnetic Force Between Parallel Currents
References
Crummett and Western Physics: Models and Applications,
Sec. 28-2, 29-1,2
Halliday, Resnick, and Walker, Fundamentals of Physics (5th
ed.), Sec. 30-2
Tipler, Physics for Scientists and Engineers (3rd ed.), Sec.
25-3
Introduction
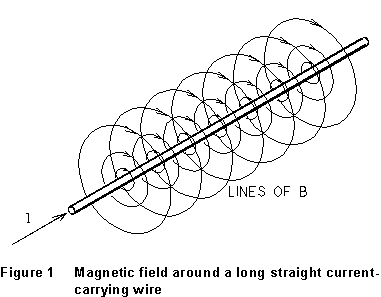 Electric current
-- moving charge -- creates a magnetic field. In particular, a current
in a long straight wire sets up a magnetic field B whose direction
at any point is tangent to a circle drawn around the wire. Fig. 1 illustrates
this. The direction of B obeys a right-hand rule:
if you point the thumb of your right hand along the current direction,
its curled fingers indicate the direction of the field lines around the
wire. The magnitude of B in this case is given by
Electric current
-- moving charge -- creates a magnetic field. In particular, a current
in a long straight wire sets up a magnetic field B whose direction
at any point is tangent to a circle drawn around the wire. Fig. 1 illustrates
this. The direction of B obeys a right-hand rule:
if you point the thumb of your right hand along the current direction,
its curled fingers indicate the direction of the field lines around the
wire. The magnitude of B in this case is given by
 (1)
(1)
where B is the field at distance d from a wire carrying
current I. The constant K depends on the units in which the
other quantities are expressed.
It is also true that a current-carrying wire placed in an external magnetic
field will experience a force due to the field. If the current is perpendicular
to the magnetic field direction, the force is perpendicular to both, and
has magnitude
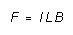 (2)
(2)
where L is the length of the wire and I the current in
it. The force direction follows from another right-hand rule: if the fingers
of the right hand are curled from the direction of I into the direction
of B, then the thumb points in the direction of the force.
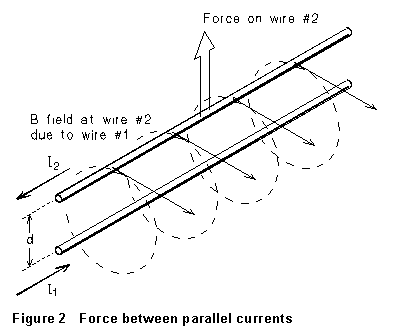 It follows that
two current-carrying wires exert magnetic forces on one another. In Fig.
2, current I1 is the source of a magnetic field at the
position of I2; the field exerts a force on I1.
(Wire 2 exerts an equal and opposite force on wire 1.) From Equations (1)
and (2), the force must be given by
It follows that
two current-carrying wires exert magnetic forces on one another. In Fig.
2, current I1 is the source of a magnetic field at the
position of I2; the field exerts a force on I1.
(Wire 2 exerts an equal and opposite force on wire 1.) From Equations (1)
and (2), the force must be given by
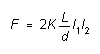 (3)
(3)
The SI unit of electric current, the ampere, is DEFINED by saying
that the constant K has the value 10-7 N/A2.
Thus if the same current I is passed through two parallel wires,
the force they exert on one another has the form
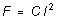
with
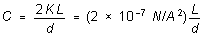 (4)
(4)
In this experiment you will use a current balance to verify the I2
dependence and check the value of the constant C predicted by Equation
(4).
Equipment
- current balance
- 6V DC power supply
- DPDT reversing switch
- current control
- ammeter (0-10 A)
- laser
- leads
Procedure
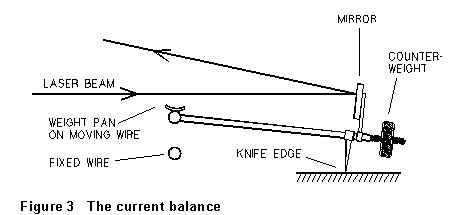 The current
balance is sketched in Fig. 3. One of the two wires is part of a frame
which balances on a knife-edge. The distance d between the two wires
at equilibrium can be adjusted by moving the counterweight. Once a value
of d is set, a small weight is placed on the pan and the movement
of the balance is observed with an optical-lever arrangement. Current to
the wires is then turned on and adjusted until the original balance position
is restored; so you have determined how much current in the wires is required
to balance a known weight.
The current
balance is sketched in Fig. 3. One of the two wires is part of a frame
which balances on a knife-edge. The distance d between the two wires
at equilibrium can be adjusted by moving the counterweight. Once a value
of d is set, a small weight is placed on the pan and the movement
of the balance is observed with an optical-lever arrangement. Current to
the wires is then turned on and adjusted until the original balance position
is restored; so you have determined how much current in the wires is required
to balance a known weight.
CAUTION: It is not hard to damage the knife edges, so consult
your lab instructor about proper procedures for adjusting and using this
instrument before you get started. The sensitivity of the balance should
be adjusted so that the heaviest weight to be used (probably 40 or 50 mg)
moves the arm down a distance slightly less than d, so that the
wires will not come into contact.
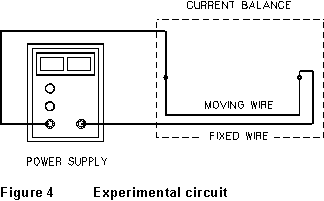
(1) Set up the circuit shown in Fig. 4. Have your instructor
check it before you plug it in. Note that the maximum current rating of
the power supply is 8 A, and it will be necessary to use currents almost
that high in the experi-ment; so you will have to use care in adjusting
the current.
 (2) Position
the laser, as indicated in Fig. 3, so that its beam falls on the wall (after
reflecting from the mirror) at a convenient height. Mount a piece of graph
paper on the corkboard provided on the wall so that the laser beam falls
on it, to use as a scale.
(2) Position
the laser, as indicated in Fig. 3, so that its beam falls on the wall (after
reflecting from the mirror) at a convenient height. Mount a piece of graph
paper on the corkboard provided on the wall so that the laser beam falls
on it, to use as a scale.
(3) Measure distances L and d and record them,
together with your estimates of their uncertainties. d should be
set at something on the order of 0.5 cm. (Remember that d is the
center-to-center distance between the wires.) Calculate the expected value
of C, from Equation (4), and its uncertainty. Record the equilibrium
position of the light beam on the scale.
(4) Place a 5 mg weight on the pan, and allow the balance to
come to rest at its new equilibrium position. Then turn on the current,
and adjust it to restore the original equilibrium position of the
balance. Turn the current back to zero, and repeat this procedure several
times to obtain an average value of I required to balance the added
weight.
Now reverse the current in the wires by turning the power supply to
"standby" and exchanging the leads at the power supply terminals;
and repeat the entire procedure. Find the overall average value for I
from both sets of data.
(5) Increase the mass on the pan in steps of 5 mg and continue
repeating procedure (4) until the balancing current reaches nearly 8A.
(6) Increase the equilibrium value of d to roughly twice what
it was, and repeat the entire procedure of steps (4) and (5) above.
Analysis
For each value of the weight in the balance pan, calculate the force
(mg) between the two currents at balance, and the overall mean value
of the balancing current and its standard error. Make a table of
F vs. I for each of the values of d. For each value of d,
draw a graph of F vs. I2, and discuss whether your data
are consistent with Equation (4). Obtain an experimental value for C
from the slope of the graph, together with an estimate of its uncertainty,
and compare it to the value calculated from Equation (4). Discuss whether
your results agree, within experimental errors, to what is expected from
(4).
The reason for reversing the current and averaging the balancing currents
you observe in both directions is to cancel out the effects of the earth's
magnetic field. Explain how this works.
Faraday's Law
last update 6/96
 Electric current
-- moving charge -- creates a magnetic field. In particular, a current
in a long straight wire sets up a magnetic field B whose direction
at any point is tangent to a circle drawn around the wire. Fig. 1 illustrates
this. The direction of B obeys a right-hand rule:
if you point the thumb of your right hand along the current direction,
its curled fingers indicate the direction of the field lines around the
wire. The magnitude of B in this case is given by
Electric current
-- moving charge -- creates a magnetic field. In particular, a current
in a long straight wire sets up a magnetic field B whose direction
at any point is tangent to a circle drawn around the wire. Fig. 1 illustrates
this. The direction of B obeys a right-hand rule:
if you point the thumb of your right hand along the current direction,
its curled fingers indicate the direction of the field lines around the
wire. The magnitude of B in this case is given by (1)
(1)  It follows that
two current-carrying wires exert magnetic forces on one another. In Fig.
2, current I1 is the source of a magnetic field at the
position of I2; the field exerts a force on I1.
(Wire 2 exerts an equal and opposite force on wire 1.) From Equations (1)
and (2), the force must be given by
It follows that
two current-carrying wires exert magnetic forces on one another. In Fig.
2, current I1 is the source of a magnetic field at the
position of I2; the field exerts a force on I1.
(Wire 2 exerts an equal and opposite force on wire 1.) From Equations (1)
and (2), the force must be given by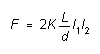 (3)
(3)  The current
balance is sketched in Fig. 3. One of the two wires is part of a frame
which balances on a knife-edge. The distance d between the two wires
at equilibrium can be adjusted by moving the counterweight. Once a value
of d is set, a small weight is placed on the pan and the movement
of the balance is observed with an optical-lever arrangement. Current to
the wires is then turned on and adjusted until the original balance position
is restored; so you have determined how much current in the wires is required
to balance a known weight.
The current
balance is sketched in Fig. 3. One of the two wires is part of a frame
which balances on a knife-edge. The distance d between the two wires
at equilibrium can be adjusted by moving the counterweight. Once a value
of d is set, a small weight is placed on the pan and the movement
of the balance is observed with an optical-lever arrangement. Current to
the wires is then turned on and adjusted until the original balance position
is restored; so you have determined how much current in the wires is required
to balance a known weight. (2) Position
the laser, as indicated in Fig. 3, so that its beam falls on the wall (after
reflecting from the mirror) at a convenient height. Mount a piece of graph
paper on the corkboard provided on the wall so that the laser beam falls
on it, to use as a scale.
(2) Position
the laser, as indicated in Fig. 3, so that its beam falls on the wall (after
reflecting from the mirror) at a convenient height. Mount a piece of graph
paper on the corkboard provided on the wall so that the laser beam falls
on it, to use as a scale.