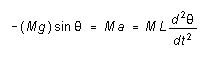| Table of Contents |
Crummett and Western, Physics: Models and Applications,
Sections
Halliday, Resnick and Walker, Fundamentals of Physics (5th
ed.), Section 16-6
Tipler, Physics for Scientists and Engineers (3rd ed.), Sections
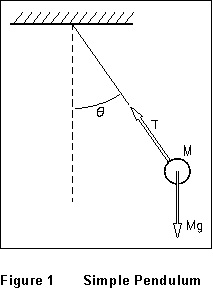A simple pendulum
is a point mass suspended by a light, inextensible string from a fixed
pivot point. The forces that act on the pendulum "bob" (mass
M) are as sketched at left: its weight Mg, and the tension
T in the suspension string. The motion of the bob, hence the net
force that acts on it, is constrained to be along the arc of a circle,
perpendicular to the string. Therefore
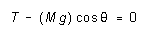
from the force components along the string, and
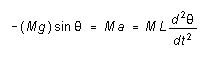
where L is the length of the string, from the components along the direction of motion.
In this experiment, we will determine the vertical component of the
tension (T cos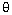
)
in the string of a pendulum at the same time we determine its angular position.
A strain gauge changes resistance when its mounting bar deflects. This
is converted into a voltage, the value of which is recorded in the computer.
At the same time, a shaft encoder is recording the angle of the pendulum.
Thus, the computer reads in simultaneously (1) the angle of the bob from
the vertical, and (2) the vertical force component exerted on the strain
gauge bar by the string. The point is to examine the dynamics of pendulum
motion carefully at two places: (1) where the pendulum stops momentarily
and turns around, and (2) the lowest point, where the pendulum is moving
the fastest.
Remember, or review before lab: (1) Newton's second law, (2) the idea of radial and tangential acceleration, and (3) the relation between linear and angular variables.
What you will be measuring is the mass of the bob, the length of the pendulum, and the angle and strain gauge force as a function of the time. Your instructor will help you configure the software on the right way. The software will record the angle vs. time directly, and also calculate the vertical component of the force exerted on the string, from a strain gauge at the pivot. Experiment with the pendulum and software data taking until you feel confident using (and knowing what the numbers mean!)
(1) Use a balance to measure the mass of the two nuts you are using in this experiment. This must be done at the beginning because both nuts are needed for 'force calibration' of the strain gauge. If the balances are busy, check that you have a loop of sewing thread with a length of about 60 cm for the pendulum. You will be mounting two nuts on this loop to act as a pendulum. If the balances are busy, you can put both nuts on the thread, hang the thread over the pulley, and measure the length [pivot to CM] carefully, with each partner doing at least one trial.
(2) Carry out the force calibration procedure in the pendulum software, once you have the masses of your two nuts. When you put the mass on the bar, make sure there is no vibration, as this will give bad calibration results. Note that the masses must be applied by being on a loop of thread hung over the pulley. The mass must be applied the same way it will be done in the actual experiment, or the calibration is no good. Also, be very careful not to disturb the ribbon cable from the shaft encoder in any way at all from the calibration to the end of the experiment. This ribbon cable from the shaft encoder also exerts a force on the strain gauge bar. As long as this force stays constant throughout the experiment, including the calibration, the computer will cancel its effect. But if you change the force applied by the cable, it throws the calculated forces off. [The effect of the sewing thread is not large: 127 cm of thread has a mass of about 0.034 gm.]
(3) Set up a pendulum of about 60 cm in length using a loop of thread and both of the nuts. Measure the length [pivot to CM] carefully, with each partner doing at least one trial. As a 'sanity check,' start the pendulum with a small (maybe 5 degrees) angle, and take data. Check the force being measured. It should be close to the weight of your bob. Tell the instructor if this does not look right.
(4) Now, do single runs with initial angles of roughly 15 and 30 degrees. One partner should do the first run, with the other partner doing the second. Each run must include at least one complete cycle of the pendulum. It's a good idea to start taking data just before a turning point. For each run, determine the angular acceleration near the turning point. (Get fairly close to the peak or trough and use a parabola fit, which assumes constant acceleration. Because the acceleration is fairly constant near the peak, you should get a good estimate of the angular acceleration.) Record this data in your lab book, being careful to include pertinent information about your procedure, and any other useful material. When you use a fit routine, please include the complete equation given on the bottom line.
At this point, each partner should draw in his or her lab book a free-body diagram of the pendulum at its turning point (the angle is a maximum or a minimum here). Each partner should decide (discussion with others is fine, of course) whether the tension in the string equals the weight of the bob. If they're not equal, you should figure out the relation from the diagram and using Newton's second law. [There are two relevant directions here: radial (along the string) and tangential. You should have a clear idea if there is any acceleration in either of these two directions.]
(5) When you have this settled, launch the bob at an angle of around 30 degrees and have the computer take data. Now plot both angle and Force vs. time. This gives you force and angle displayed on the same graph, with numerical values. Look at a �turning point' in this data (where the angle goes through a maximum or a minimum), and write down the angle and force, even though these may not be totally precise. From your knowledge of what's going on, make a numerical calculation of what the measured force should be at this spot, where the bob is turning around. [Keep in mind that the measured force is only the vertical component at the end of the strain gauge bar.] This calculated force should agree with the measured value on the graph within 1 or possibly 2 percent. [Keep this data on the screen while doing the next part.]
Each partner should draw in his or her lab book a free-body diagram of the situation when the bob is moving through its lowest point. Each should decide if the tension is equal to the weight of the bob, should be larger, or should be smaller. (In the process, each partner must decide if there is any tangential or radial acceleration at the lowest point.)
(6) When you are sure you know what's going on, and if time permits, repeat the single runs with launch angles of roughly 15 and 30 degrees. This will show whether the first values obtained are generally repeatable. [The conditions should be within 10 or 20 percent of the initial runs, and the results should lie within 10 or 20 percent of the initial results.] If there is some strange data somewhere, you may be able to use a 'comparable' run. If all the data is good, use it all, unless very short of time. Last, re-do the 'sanity check' of pendulum weight.
The analysis should relate experimental quantities to one another and to the theory. You have already done this in lab by predicting the measured force at the turning point based on other measured values (mass, length, etc.).
(1) You should calculate the tangential acceleration from the measured angular acceleration at the turning point. This 'experimental' value should be compared to a 'theoretical' value you obtain from other experimental parameters (mass, force, length, angle, etc.).
(2) You should determine a 'theoretical' value of the force at the lowest point based on some of the parameters you measured (angle, angular velocity, length, etc.). This should compare within a few percent of the measured force at the lowest point.
(3) Include a Table of Results in your report which compares the three just-mentioned quantities for each of the runs you did.
Conservation of Linear Momentum
updated 7/97