CSSE 120 — Introduction to Software Development, Robotics

Reminder: for each class session and associated homework:

• Where you do your work: In Eclipse in the project that you checked out for that session.
• How you turn in your work: You commit that project, as follows:
  • Right-click on the project name in the Pydev Package Explorer view.
  • Select Team → Commit
  • In the message box that appears, put a message to yourself if you wish (eventually, these messages will be for your teammates) and press OK.
  Commit OFTEN, not just when you finish the homework. Doing so provides easy backups of your work.
• How you can keep track of what you have completed:
  • As you finish each TODO, change the word TODO to DONE.
  • When you finish ALL your work in a project, right-click on the project name and Rename the project by adding Done to the beginning or to the end of the project name.
    • Keep the rest of the project name unchanged, to keep things simple.
    • You choose whether to place Done at the beginning or end of the project name, depending on how you like the projects sorted.
    • The exact phrase Done is not important; any phrase that helps you remember that you have done the project is fine.
  • If you have questions: Email csse120-staff@rose-hulman.edu.
  • Best place and time to do the homework:

    CSSE lab (Moench Hall, room F-217) OR Olin 269
    7 p.m. to 9 p.m.
    Sunday — Thursday.

Main learning objectives for this homework:

• Understanding and applying range expressions.
• Objects and classes:
  • The concept: Classes are types; objects are instances of classes; objects know things and can do things.
  • How to construct objects (instances of classes)
  • How to apply methods to objects
  • How to reference instance variables of objects
• Continue our introduction to counting loops (FOR statements with RANGE expressions)
• Understand why functions are important:
  • They encapsulate ideas (i.e., bundle them under a single name).
  • They hide information (especially variable names).
  • Their parameters give them power.
  The main goal of this homework is to see first-hand the power of parameters.

Additional learning objectives for this homework:

• Continue to get familiar with Eclipse (your IDE — Integrated Development Environment)
• Continue practicing how you get projects from your SVN repository and turn them in: Checkout and commit .
• Continue understanding the basic structure of a Python program in our style: main, which calls other functions.
• Continue practicing the input/compute/output pattern:
  • Prompting for and getting input from the user
  • Using variables to store values
  • Printing strings and the values of variables
• Continue practicing the distinction between defining functions and calling functions
• Continue practicing the distinction between printing and returning a value

Do the following exercises, using today's project: Session04_FunctionsMethodsAndParameters

1. If there is any previous homework that you have NOT finished (or that you have questions about):
   • HW 1
   • HW 2
   • HW 3
   then make an appointment NOW to meet with your instructor or an assistant. You definitely want to be caught up by Thursday. Working one-on-one with your instructor or an assistant is the fastest way to do so.
2. If you think that it will be helpful, study the examples in the following modules from today's project:
   • m1_defining_and_calling_functions.py
   • m2_input_compute_output.py
   • m5_parameters_arguments_and_return.py
   Nothing to turn in for this problem.
3. Do the TODO's in the m3_range_expresssions.py module of today's project, if you did not complete them in class.
4. Do the TODO's in the m4_objects_and_classes.py module of today's project, if you did not complete them in class.
5. Do the TODO's in the m6_parameters.py module of today's project, if you did not complete them in class.
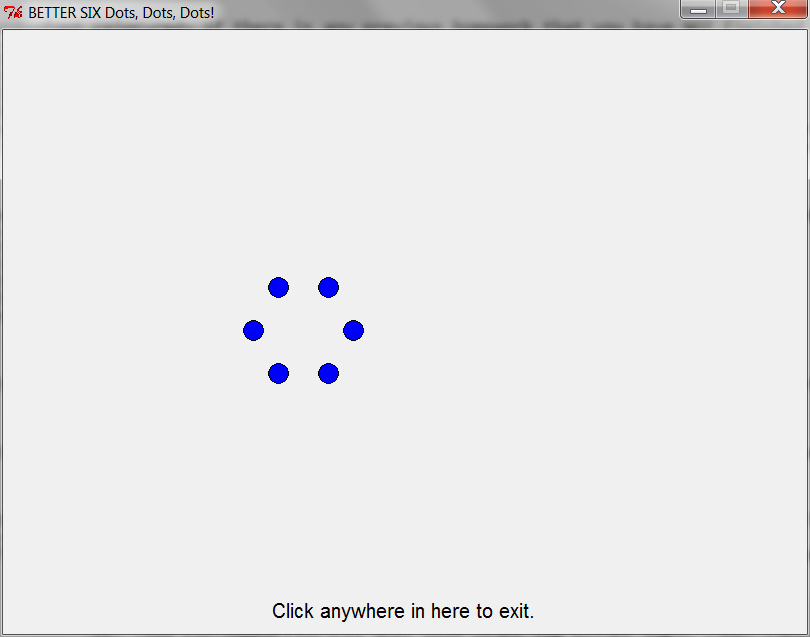
   • Here are pictures showing what your code should produce from the tests provided in main.

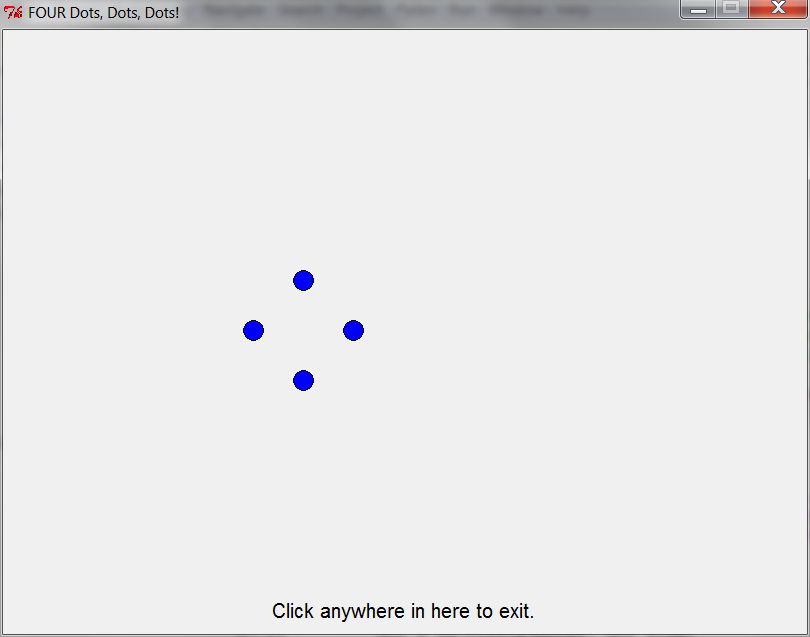
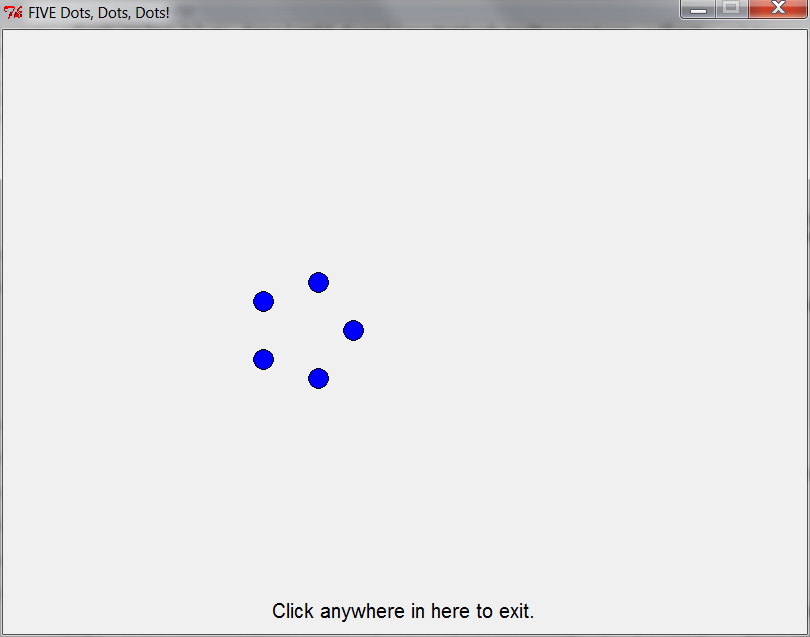
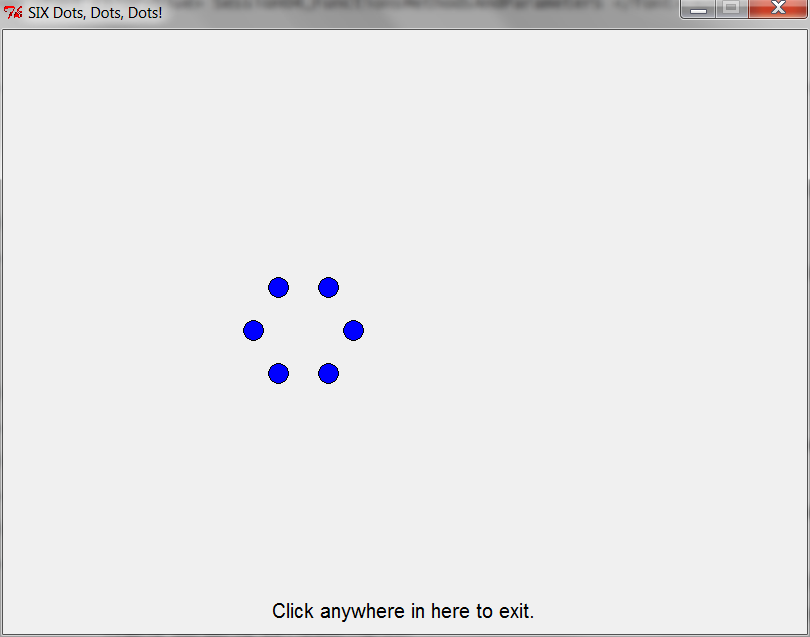
     four_dots()	five_dots()	six_dots()	close_window()
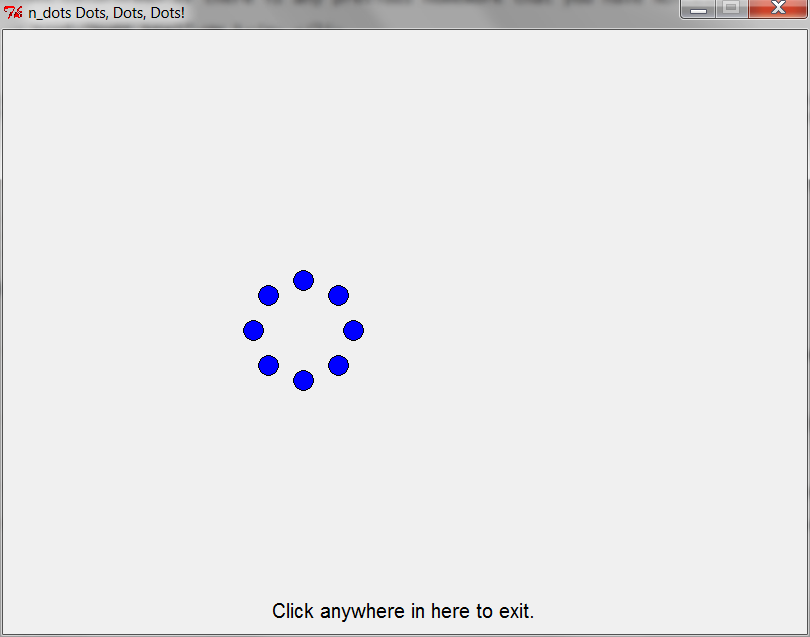
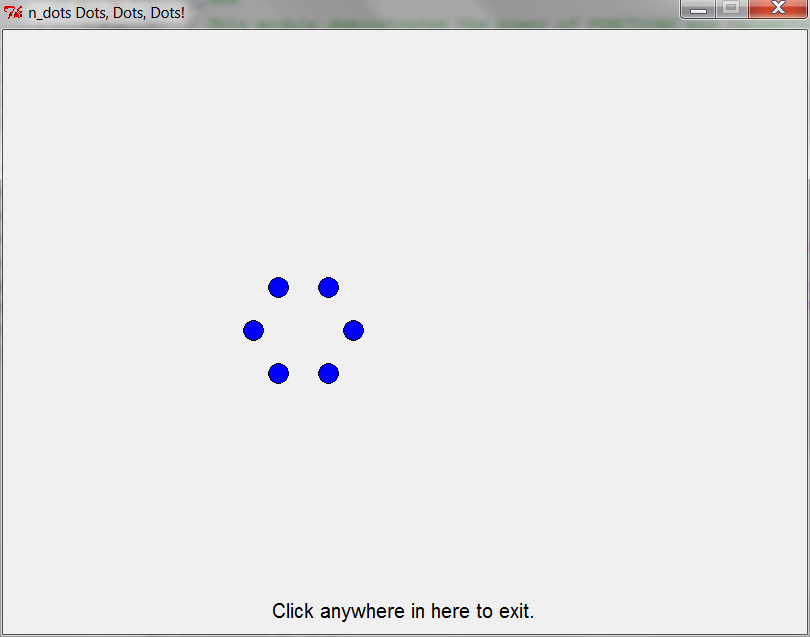
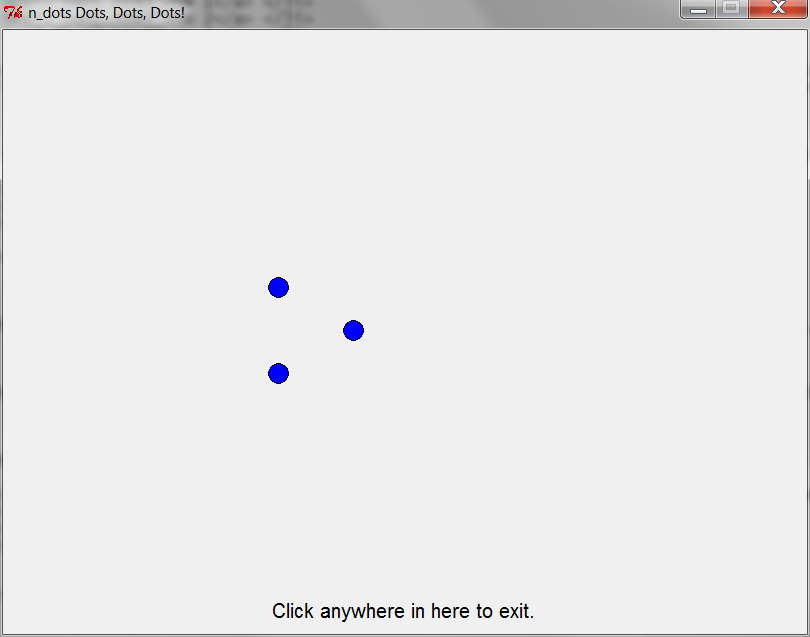
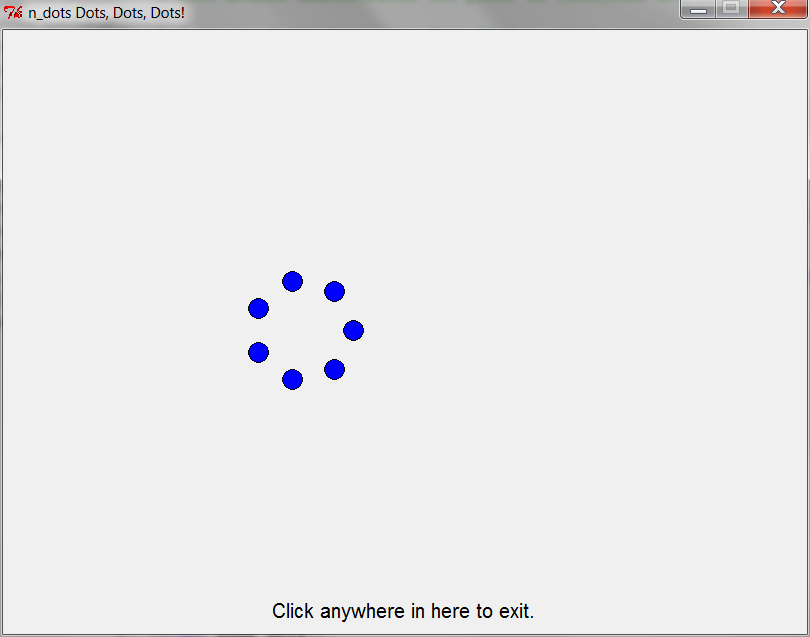
     better_six_dots()	n_dots(8)	n_dots(3)
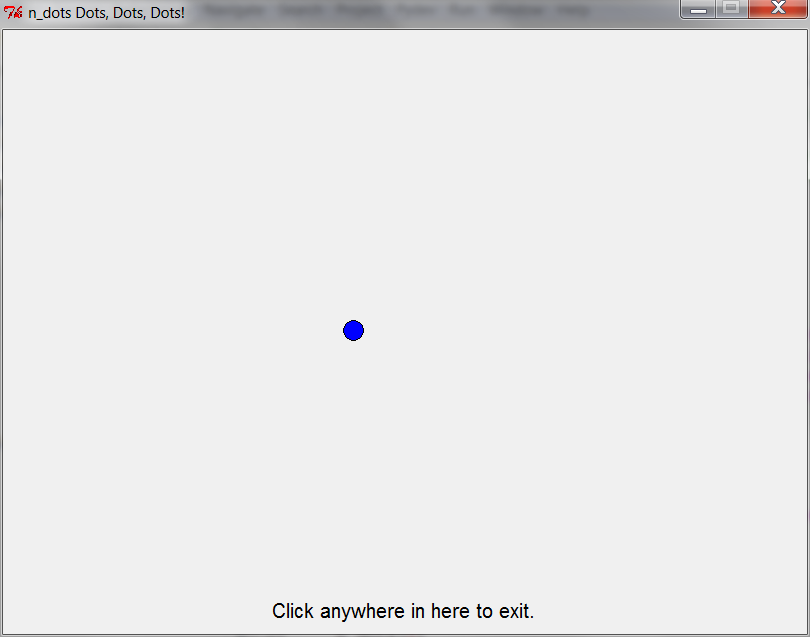
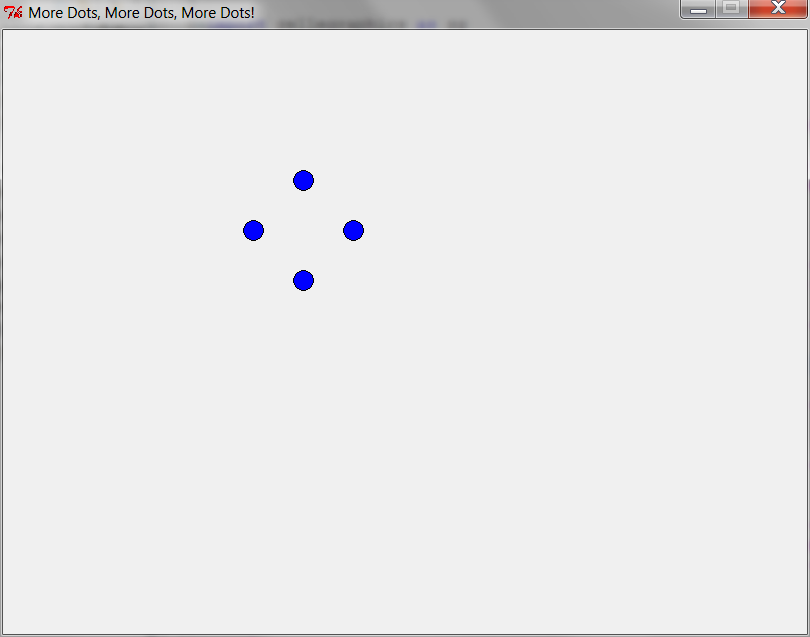
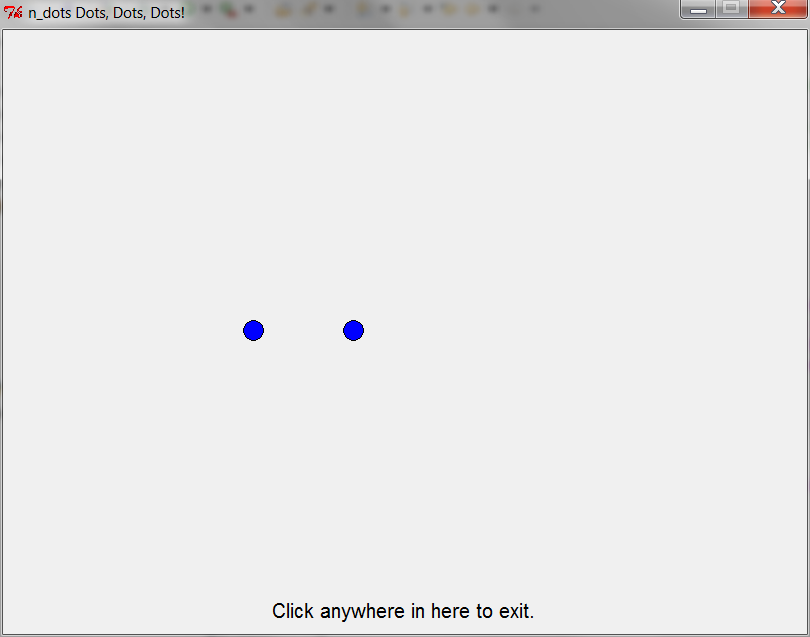
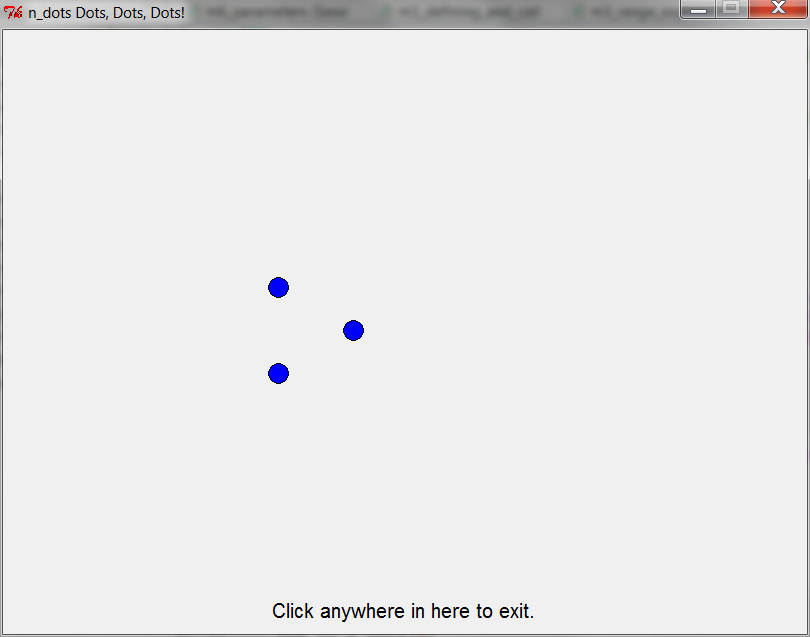
     one_to_n_dots(4) — 1st time through loop	one_to_n_dots(4) — 2nd time through loop	one_to_n_dots(4) — 3rd time through loop	one_to_n_dots(4) — 4th time through loop
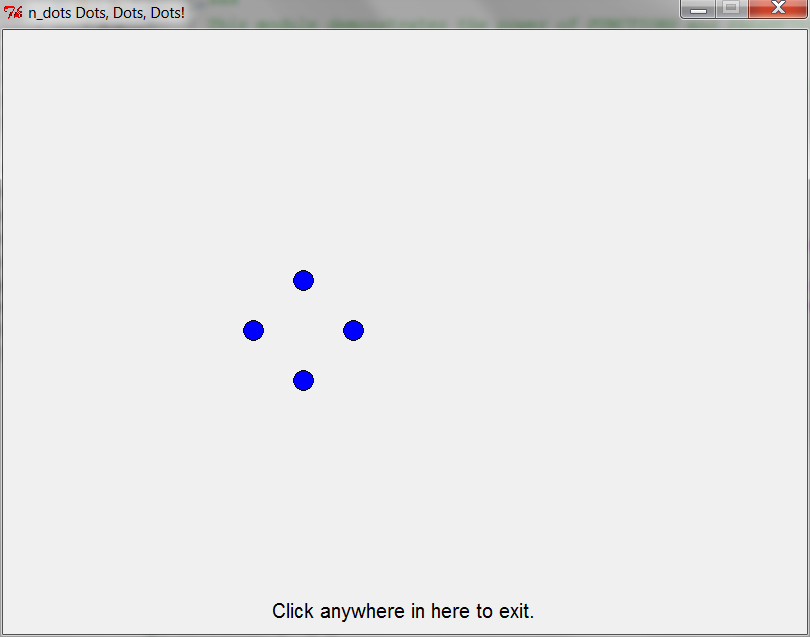
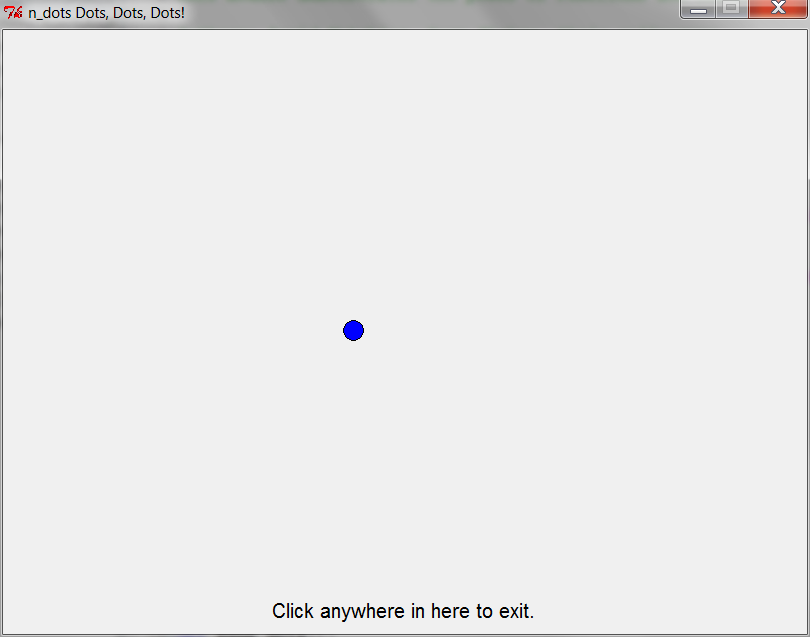
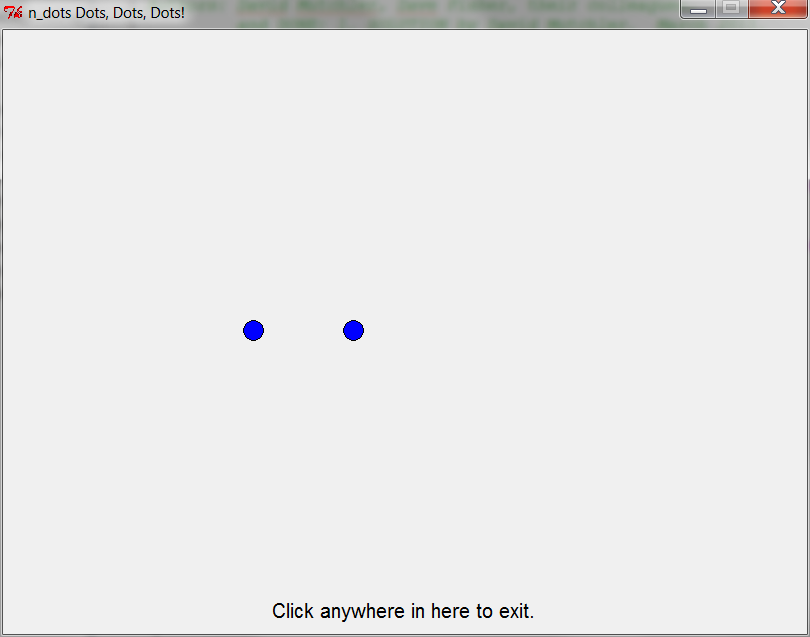
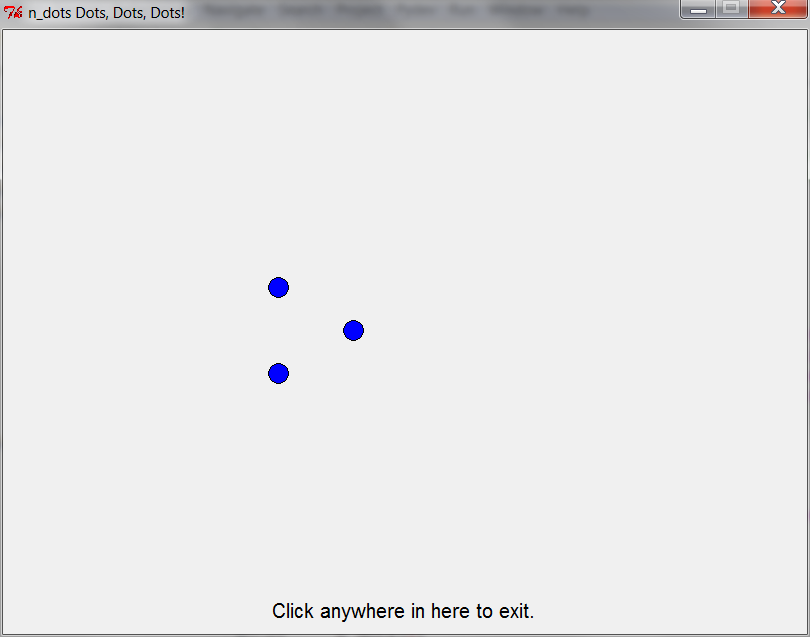
     one_to_n_dots(7) — 1st time through loop	one_to_n_dots(7) — 2nd time through loop	one_to_n_dots(7) — 3rd time through loop	one_to_n_dots(7) — 4th time through loop
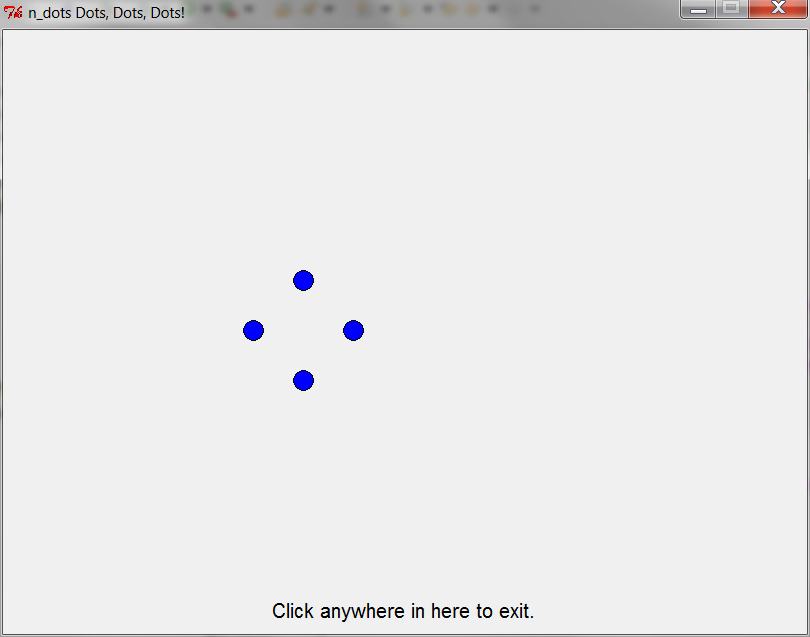
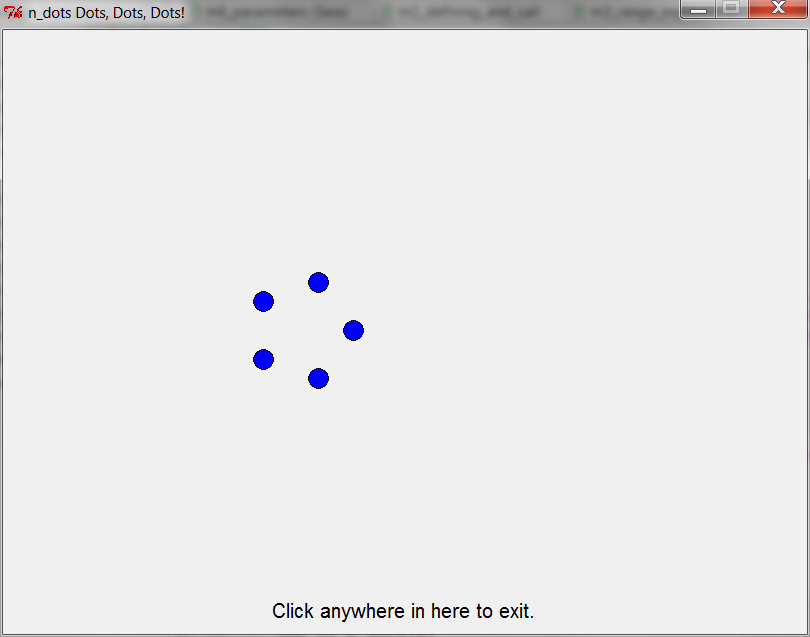
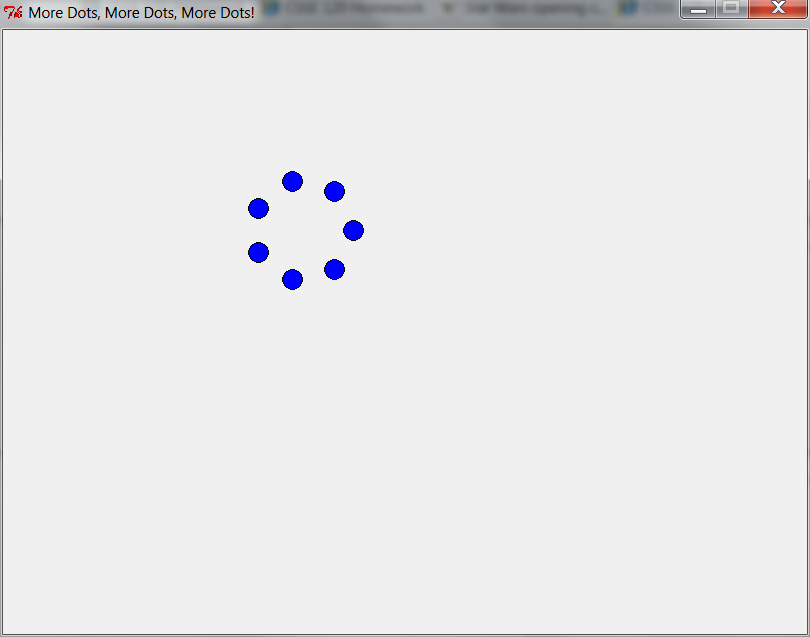
     one_to_n_dots(7) — 5th time through loop	one_to_n_dots(7) — 6th time through loop	one_to_n_dots(7) — 7th time through loop

6. Do the TODO's in the m7_parameters.py module of today's project, if you did not complete them in class. But see the following two NOTE's.

   • NOTE: Here are pictures showing what your code should produce from the tests provided in main.

     n_dots(window, 7)	n_dots(window, 4)	n_dots(window, 7)   and n_dots(window, 4) (both tests, together)
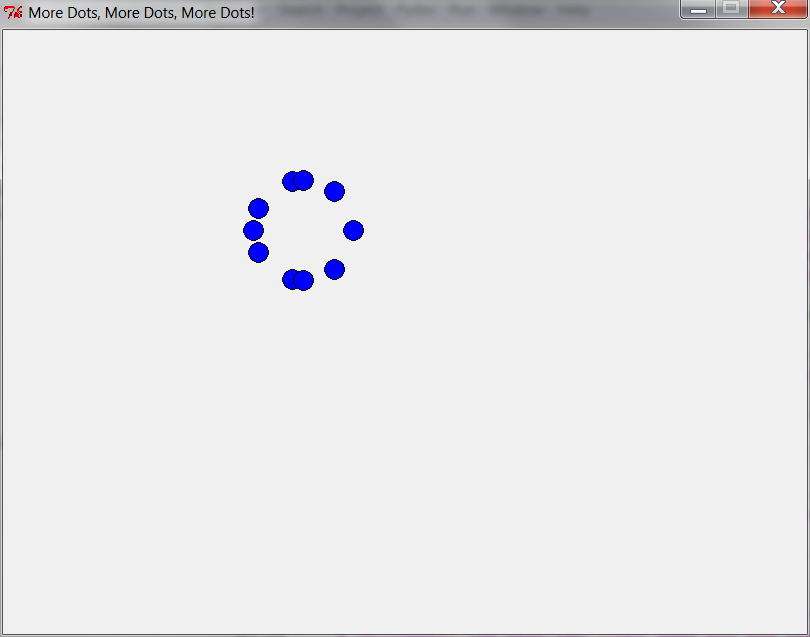
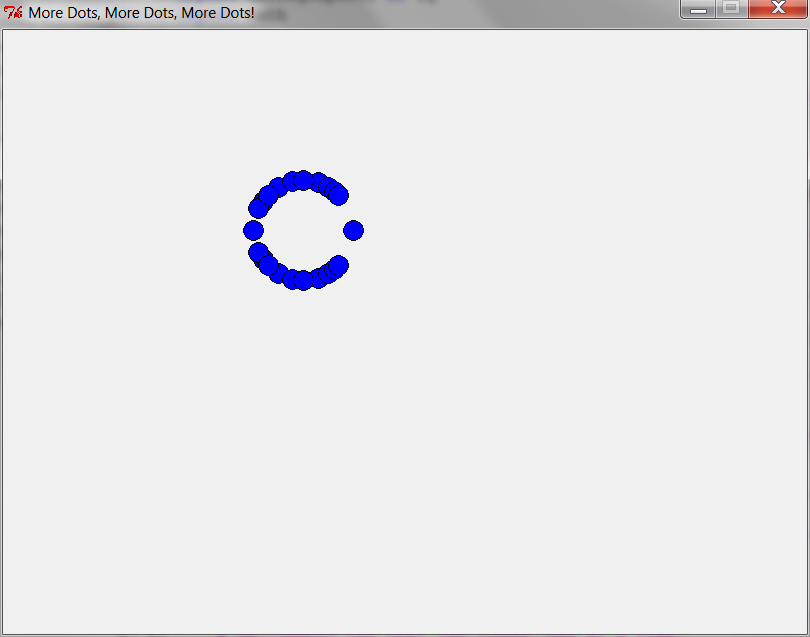
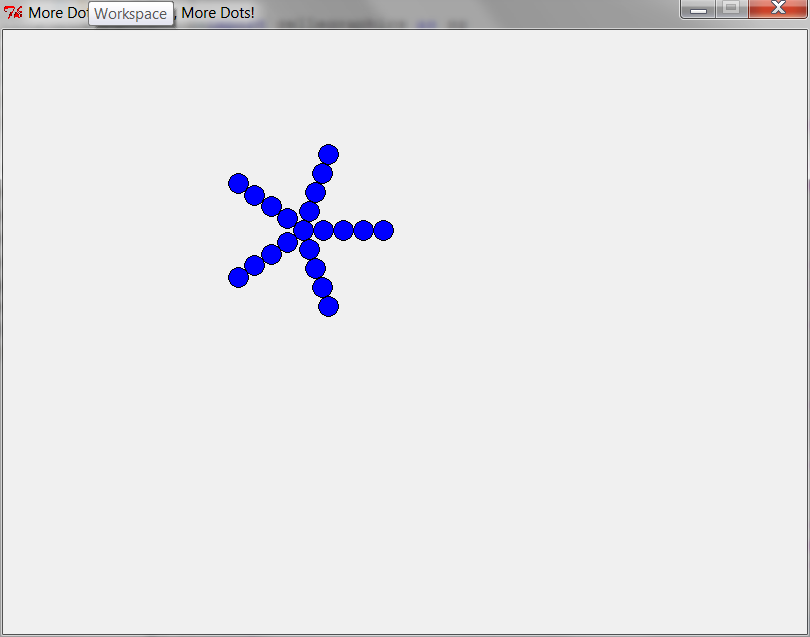
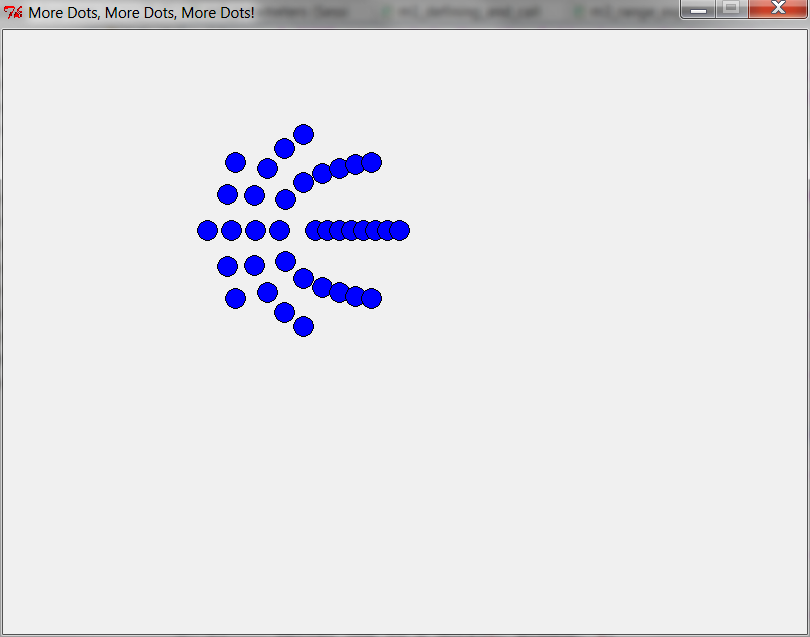
     one_to_n_dots(window, 8)	for k in range(5): better_n_dots(5, window, k * 20)	better_one_to_n_dots(8, window, 4)	better_one_to_n_dots(8, window, 8)

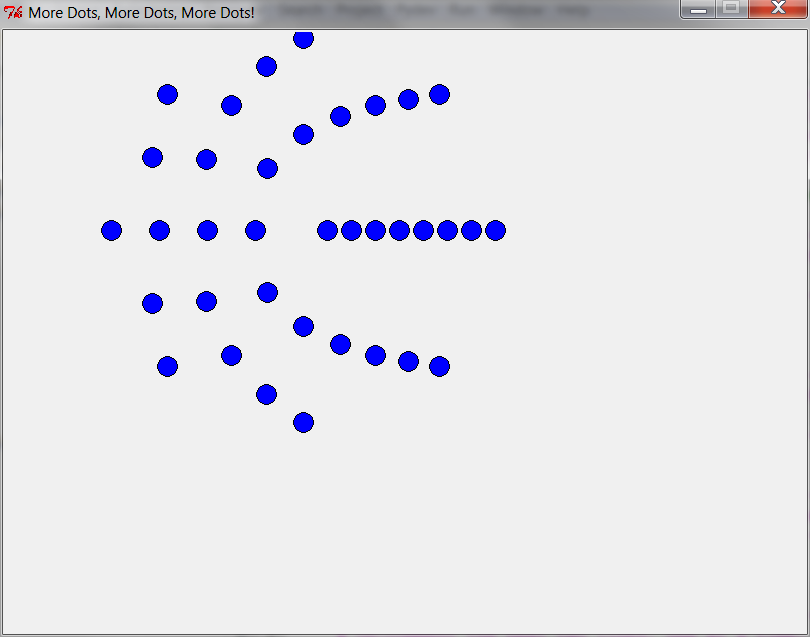
   • NOTE: For best_n_dots, the instructions say:

     
         # TODO: 6. Implement and test this function.
         #          In testing it, draw at least 5 interesting shapes,
         #          by calling this function inside simple loops.  The 5 shapes
         #          should all appear on the same window without overlapping. (But
         #          any one of your shapes can certainly have things overlapping.)
     
     

     By this, we mean for you to put a simple loop in main that calls best_n_dots, using the loop variable to change the values of the arguments passed to best_n_dots.

     For example, here is the code that one student (Ryan Landwehr) put into main to test his best_n_dots:

         center = zg.Point(200, 200)
         dot_size = 10
         for k in range(5):
             best_n_dots(5, window, center, k * 20, dot_size * k)
     

     The above code produced the following picture:

     

     Beautiful, isn't it!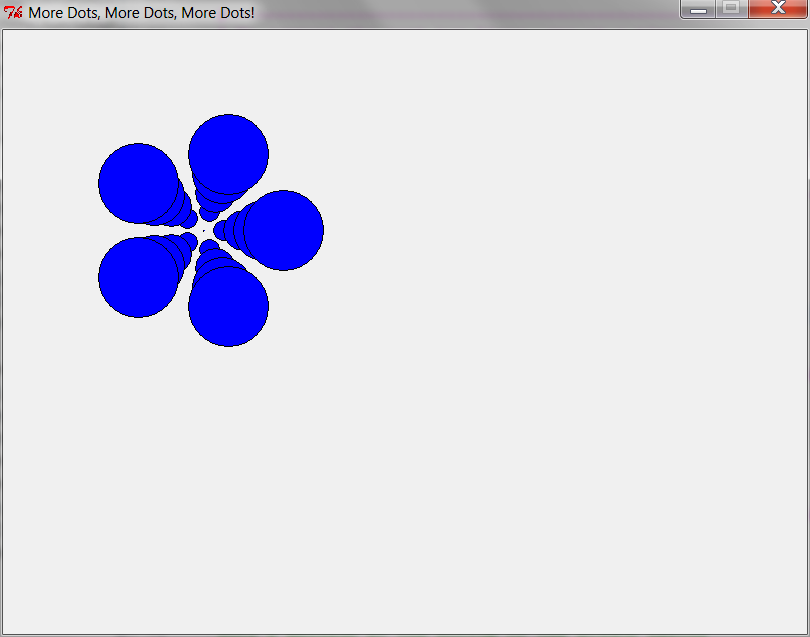

     You should do similarly, playing around with where you put the loop variable (k in the above code). Make 5 such loops (you can use the above as one of them, if you like), in hopes of getting 5 “interesting” pictures. Almost anywhere produces something that I would find interesting!

7. Consider the following two functions:

   def weak_dots(window): n = 10 center = zg.Point(200, 200) radius = 50 dot_size = 10 for k in range(n): # n points, at 0, 2*pi/n, 2 * (2*pi/n), 3 * ..., radians theta = k * 2 * math.pi / n # theta is the angle in radians x = center.x + radius * math.cos(theta) # Polar coordinates to x/y y = center.y + radius * math.sin(theta) point = zg.Point(x, y) dot = zg.Circle(point, dot_size) dot.setFill('blue') dot.draw(window)

   def strong_dots(window, n, center, radius, dot_size): for k in range(n): # n points, at 0, 2*pi/n, 2 * (2*pi/n), 3 * ..., radians theta = k * 2 * math.pi / n # theta is the angle in radians x = center.x + radius * math.cos(theta) # Polar coordinates to x/y y = center.y + radius * math.sin(theta) point = zg.Point(x, y) dot = zg.Circle(point, dot_size) dot.setFill('blue') dot.draw(window)

   The above two functions are identical except for the parts marked in red.

   Which of the above two functions is more powerful? Why? What makes it more powerful?

   There is nothing to turn in for this problem, but the above question is important, so make sure that you see the point. If not, ask in class!