Rationale. The notion of a space station located at a 'stable' point in space has some appeal for space exploration because no energy needs to be expended to keep the space station there.

The determination of conditions for stability at one of the so-called 'Lagrange points' is in fact rather complicated, as the following development will show. The combination of inherent interest and considerable difficulty makes this appealing as a vehicle for students to sometimes pool their talents to understand various parts of the work, and at other times work by themselves on other parts.

This problem illustrates several key components of a theoretical mechanics course, and offers a chance to reinforce many of the concepts already introduced:

• the way things are worked out in a rotating coordinate system
• the way vectors are employed in gravitational force calculations (which parallels the way vectors are employed in electrostatic force calculations)
• the expansion of functions in terms of small quantities
• the solution of a complicated oscillatory system, where one obtains frequencies and normal modes of oscillation

• Ideally students would have been introduced to the development of fictitious forces in a rotating frame, and would have done some straightforward problems.
• Ideally students would have dealt with one-dimensional coupled oscillations

The Lagrange restricted 3-body problem.
 

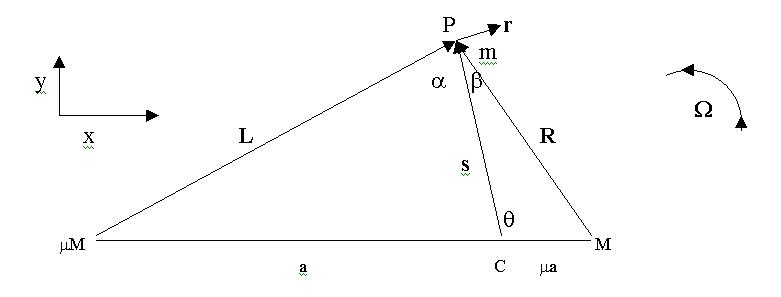
Masses M and m M revolve counterclockwise with angular velocity W about their common center of mass (CM) at C. The distance between them is a(1+m ). The parameter m can either be taken as much larger than 1 or much smaller than 1. We will treat it as much smaller: m << 1 .

We first search for a point of 'static' equilibrium P for a tiny mass m ( m <<M ). This means that the vector sum of the two gravitational forces on m must lie along the line from P to C, pointing toward C. The magnitude of this net force must also equal mW²s, the centripetal acceleration of m at point P in the rotating coordinate system.

Both M and m M revolve around their common CM at C. The gravitational attraction must provide an acceleration W²x, where x is the distance from the object (either M or m M) to the CM at C.

Exercise 1. Use Newton's second law to show for either mass M or m M that

(0)                W² = (GM/a³)/(1+m )²

where G is the gravitational constant 6.67 x 10^-11 N-m²/kg² .

Exercise 2. Use Newton's second law for a mass m at point P and show that

(1)                 - GmMR/R³ - Gmm ML/L³ = - mW²s

(Bold face characters represent vectors.)

We may take components of this vector relation in any coordinate system. In the x-y system we get

(2)                 - GmMR_x/R³ - Gmm ML_x/L³ = - mW²s_x

(3)                 - GmMR_y/R³ - Gmm ML_y/L³ = - mW²s_y

Finding the equilibrium point P. In a polar coordinate system centered at C, the components of the forces perpendicular to s must add to zero.

Exercise 3. Use this condition to show that

(4)                 GmM sin b /R² - Gmm M sin a /L² = 0

Exercise 4. Use (4) and another relation to show that L=R (the triangle of the three masses must be isoceles).

We may also sum the gravitational force components along s, to give

(5)                 GmM cos b /R² + Gmm M cos a /L² = mW²s

Exercise 5. Using L=R and the law of cosines, show that

(6)                 s² = R² - m a²

Exercise 6. Using (0), (5) and (6) and L=R show that the triangle of the three masses must be equilateral

(7)                 R = L = a (1+m )

Stability of small oscillations about the equilibrium point P.
Now we must see if the equilibrium is stable for small displacements r of mass m from point P. The vector r will have rectangular components x and y, while the velocity v = dr/dt will have rectangular components v_x and v_y, and the acceleration a =d²r/dt² will have rectangular components a_x and a_y.

We shall do the calculation in a coordinate system (x,y) which rotates about the system CM at C with a constant angular velocity W (W points in the +z direction). In a rotating coordinate system several 'fictitious' forces appear. Here are the two which appear in our problem

(8)             the coriolis force         -2m W x v

(9)             the centrifugal force     -m W x (W x (s+r))      =         m W² (s+r)

The total gravitational force on the tiny mass m from the two large masses M and m M is

(10)                F_grav = -GmM(R+r)/(R² + r² + 2r· R)^3/2 - Gmm M(L+r)/(L²+ r² + 2r· L)^3/2

For small values of r, we will keep only terms up to first order in r (like x and y, but not including x², xy, or y² and higher powers of x and y). The theory will then be valid for r << a.

Exercise 7. Using (0) and (7) show that (10) can be written

(11)                F_grav = -[mW²/(1+m )] [(R+r)/(1+(r/R)²+2r· R/R²)^3/2 + m (L+r)/(1+(r/R)² + 2r· L/L²)^3/2]

Exercise 8. Expand (11) in a series to first order in r, and show that to this approximation

(12)               F_grav = -mW² r - mW² [R+mL]/(1+m ) +3mW² [R(r· R) + mL(r· L)]/[R²(1+m )]

Exercise 9. Use (0), (1) and L=R to show that

(12')                 -mW² [R+mL]/(1+m ) = -mW² s , or that [R+mL]/(1+m ) = s

Using Newton's second law in the rotating coordinate system with the fictitious forces gives

(13)                 m a = F_grav + mW²(s+r) -2m W x v

Exercise 10. Show that (13) reduces to

(14)                 m a = -2m W x v + 3mW²[R(r·R) + mL(r·L)]/[R²(1+m )]

Exercise 11. Given R = L = a(1+m ), show that the x-component of (14) is

(15)                 ma_x = -2m (W x v)_x + 3/4 mW²[(1+m )x + (m -1)Ö 3 y]/(1+m ) , or

(15')                 a_x = +2 W v_y + 3/4 W²[ x + Ö 3 y (m -1)/(m +1)]

Exercise 12. Calculate the y-component of (14)

Let x = A exp(iw t) and y = B exp(iw t), where A and B can be complex numbers. It is understood that at the end we will take the real part of A exp(iw t) to represent x and take the real part of B exp(iw t) to represent y.

Exercise 13. Show that (15') becomes

(16)                 A(-w² - 3/4 W²)                                         +B(-2iwW -3/4 W²Ö 3 (m -1)/(m +1) ) = 0

Exercise 14. Show that the y-component of (14) leads to the equation

(17)                 A(+2iwW -3/4 W²Ö 3 (m -1)/(m +1) )         +B(-w² - 9/4 W²)                                    =0

Equations (16) and (17) have a trivial solution if A = B = 0. For a non-trivial solution of (16) and (17) we must have the same ratio A/B from each equation.

Exercise 15. Show the non-trivial solution of (16) and (17) is a solution of

(18)               w⁴ - w²W ² + 27/4 W⁴ m /(1+m )² = 0

Exercise 16. Show the solution for w as a function of m is

(19)                 (w /W )² = 1/2 ( 1 ± Ö [1-27m /(1+m )²] )

Exercise 17. Show that for w to be real, m must satisfy the inequality

(20)                 (1+m )² ³ 27 m

Exercise 18. For the Earth-Moon system, m = M_moon/M_Earth = 0.0123 .
a) Decide if there could be stable equilateral-triangle orbits for the Earth-Moon system.
b) Determine the range of possible m values for stable equilateral-triangle points
c) Determine the range of possible w /W values for stable equilateral-triangle points

Exercise 19. Find the complex ratio A/B when w /W has the lower of its two values in (19) for the Earth-Moon rotating system.

Exercise 20. Using the complex ratio A/B from the previous exercise, find solutions of the form

                x=c cos(w t + f )         and         y = d cos(w t + q ),

where w , c, d, f , and q are all real constants. Find the numerical values of c, d, f , and q , or find ratios or differences of these quantities. (Your solution is one of the small-amplitude normal modes of oscillation of a tiny mass m about its equilibrium point P.)