Advanced Laboratory and/or Lecture Demonstration Apparatus Competition
and Low Cost Competition

Apparatus Title: Apparatus Demonstrating the Dynamics of the Chatter Ring Toy

Abstract : This apparatus confirms a new theory explaining the motion of the Chatter Ring toy. It provides a new, simple, and hands-on means for students to explore combined rigid body translational and rotational dynamics, and has added interest due to its relation to the toy.

Description: In his column "How Things Work", Crane[1] examined the Chatter Ring toy consisting of five beads on a circular rod and described the peculiar spinning and wobbling motion of the beads. It is now available under the name Gyro Ring from a science education supply company[2], which advertises "Guaranteed to keep your students enthralled for hours." Indeed, there are web pages devoted to dozens of "tricks" which can be performed with this toy. Until recently, however, there has been no successful explanation of how the Chatter Ring actually works. The apparatus described here confirms a new theory explaining the motion of the toy[3]. It provides a new, simple, and active means for students to explore rigid body translational and rotational dynamics, and has added interest due to its relation to the toy.

The new theory proposes that each bead contacts the rod twice, not once as in a hula-hoop: first at the top of the bead and again at the bottom, but offset at an angle around the inner circumference from the top contact. The contact points determine the orientation of the bead on the rod, and the motion consists of the bead rolling on the surface of the rod around an instantaneous axis through them. As the bead rolls, the contact points trace a double helix on the surface of the rod.

For simplicity the theory models the bead by a thin washer of inner radius a and the ring by a straight cylindrical rod of radius b. Rigid body dynamics then yields the prediction[3]

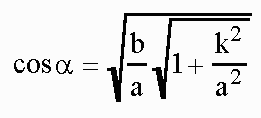
where alpha is the pitch angle of the double helix traced by the contact points and k is the radius of gyration of the washer, about a diameter.

The apparatus shown in Fig. 1. tests this relation. The straight cylindrical rod consists of a 5-ft long, 3-in diameter PVC pipe wrapped first with four 8.5" x 11.5'' sheets of carbon paper taped securely in place facing outwards and then with a single long sheet of white paper from a 15"-wide roll of newsprint from a craft store. Perform the experiment by setting a washer in motion on the rod. As the washer moves, its points of contact with the rod produce a carbon paper trace on the white paper. Removing the paper and examining the trace reveals a double helix with constant pitch, confirming the proposal that there are two contact points. Measuring the pitch angle alpha of the helixes with a protractor provides an experimental confirmation of the formula above.

To set a washer in motion, use one hand at the top of the PVC pipe to hold it in a vertical position with the bottom pressed firmly on the floor to prevent the pipe from wobbling. It helps to also press the top against a firm support such as a projecting tabletop. Use the other hand to hold one side of the washer so that two points on the far side are in contact with the surface of the pipe. Then just swing the hand down around the instantaneous axis of rotation through the two contact points.

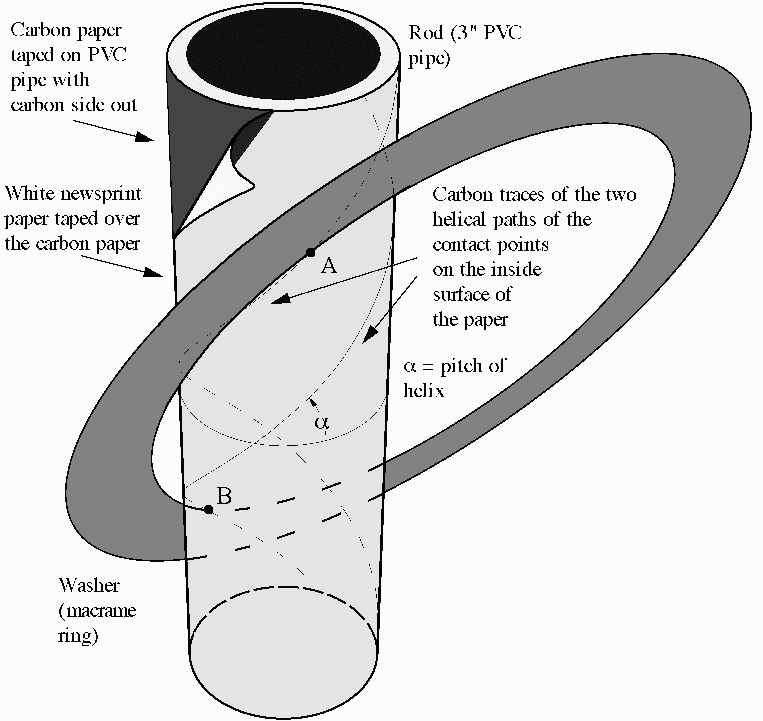
Figure 1.  The washer and rod apparatus.  Points A and B are the two instantaneous points of contact of the washer with the rod.  They determine the instantaneous axis of rotation of the washer rolling on the surface of the rod, and their forces on the white paper produce carbon paper traces of their paths.

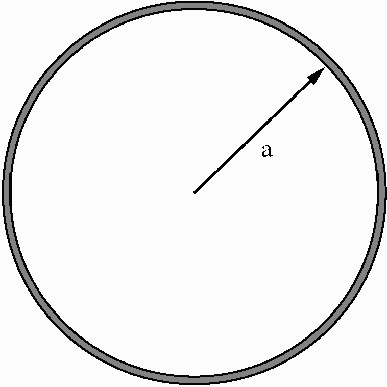
Figure 2. The first set of "washers"consists of nominally 5, 6, 7, 8, 9, 10, and 12 - inch diameter brass macrame rings bent from 1/8 - inch brass rod. Larger craft stores sell these macrame rings in many sizes.

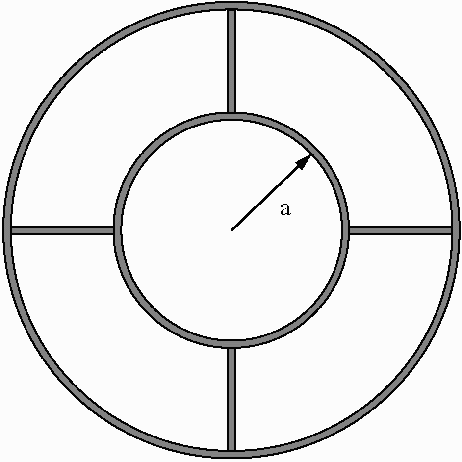
Figure 3. One of the second set of "washers", composed of two macrame rings joined with posts cut from 1/8 - inch brass rod. The inner ring is 7 inches in diameter in all cases. The outer rings are 9, 12, 14, and 16 inches in diameter. The first "washer" of this set is simply a 7 inch diameter ring.

There are two different sets of "washers". The first, shown in Fig. 2, consists of circular brass macrame rings from a craft store. In this case the radius of gyration about a diameter is approximately k = a/sqrt(2), and the formula for the pitch angle reduces to

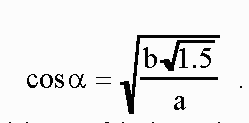
(This is only approximate because of the thickness of the brass ring, which makes the inner diameter of the ring slightly different from the average diameter of the ring.)

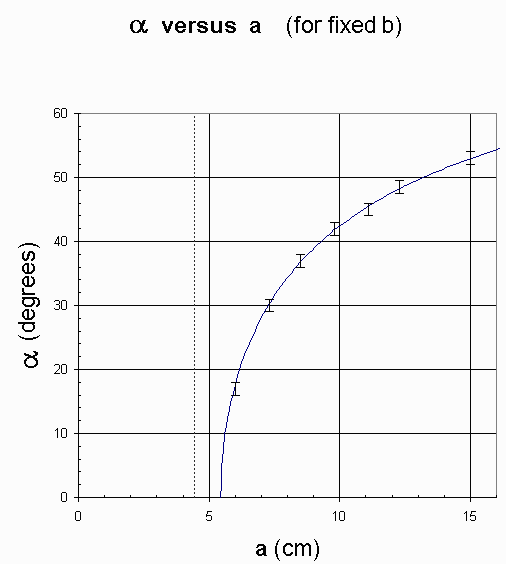
The following figure compares experimentally measured values of alpha for different values of a to the theoretical graph of alpha versus a for fixed b as predicted by this equation.

Each "washer" of the second set consists of two concentric macrame rings joined by four brass posts so as to minimize air resistance as shown in Fig. 3. They all have the same diameter inner ring, but the diameter of the outer ring increases progressively. Thus the inner radius a of these double-ring "washers" is the same for all, but the radius of gyration k increases progressively. This radius of gyration can be calculated from the geometry of the double ring and its joining posts, or, alternatively, by timing the period of simple harmonic motion of the double ring when suspended from its rim on a knife edge in the usual manner.

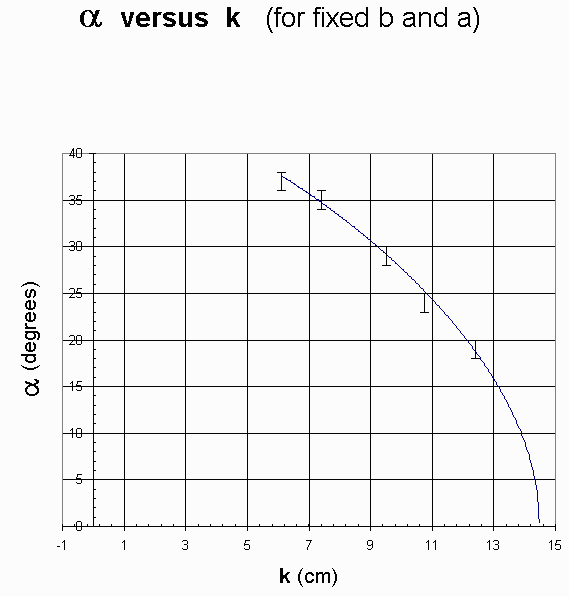
The following graph compares experimentally measured values of alpha for different values of k to the theoretical graph of alpha versus k for fixed values of a and b as predicted by the first equation:

In conclusion, this apparatus provides a new way for students to examine combined translational and rotational rigid body dynamics. The apparatus is very simple, and the experiment is very simple to perform. Finally, the apparatus may attract students' interest because it shows how the Chatter Ring toy works.

References

1. H. Richard Crane, Phys. Teach. 30, 306 (1992)

2. Order Number P3-3600, $11.00, from Arbor Scientific, P.O. Box 2750, Ann Arbor, MI 48106-2750.

3. To be submitted for publication.