Advanced Laboratory and/or Lecture Demonstration Apparatus Competition

Apparatus Title: String & Springs: A mechanical analogy for one-dimensional quantum physics.

Abstract Standing waves on a string are often used to introduce the ideas of stationary states in quantum physics but they cannot produce the wave functions of classically forbidden regions. The String & Springs apparatus overcomes this shortcoming allowing mechanical demonstration of wave functions for a wider range of physical situations.

String & Springs: A mechanical analogy for one-dimensional quantum physics.

Introduction. We often use the analogy of standing waves on a string with fixed ends to introduce the ideas of one-dimensional stationary states in quantum physics. This mechanical demonstration can be used to discuss many of the important properties and behaviors of a quantum system. The analogy is especially compelling since the shapes of standing waves on the string are essentially identical to the shapes of the spatial part of stationary state quantum wave functions for a flat bottomed infinite potential energy well. This simple demonstration can even be extended to simulate wave functions for other potential energy diagrams by using small weights to vary the linear mass density along the length of the string. However, there is one major shortcoming of the stretched string analogy - it cannot produce quantum wave shapes like those found in classically forbidden regions. The String & Springs apparatus overcomes this shortcoming allowing mechanical demonstration of quantum wave function shapes for a much wider range of physical situations.

Theory. The shape of the spatial part of one dimensional stationary state quantum wave functions is determined by the time independent Schrödinger equation :

Equation 1 The shape of standing waves on a string with angular frequency, omega, linear mass density, µ(x), and stretched with a tension, T, is determined by the following equation : Equation 2 These two equations have the same basic structure and thus will have the same solutions if we choose µ(x) to satisfy: Equation 3

The equivalence of equations 1 and 2 is what makes the stretched string a good analogy for the quantum wave function. But equation 3 points to the shortcoming of the analogy. The left hand side of equation 3 is positive definite, whereas the right hand side can be positive or negative depending on whether we are considering a classically allowed region or a classically forbidden region. So although the two equations are mathematically equivalent, physically the stretched string of equation 2 can only simulate classically allowed regions of equation 1. The String & Springs apparatus overcomes this shortcoming by using springs to add an extra term to equation 2. The stretched string is suspended between ridged bars running parallel to it by means of a number of springs running in a perpendicular direction from the string to the bars.

Equation 4 Here s(x) is the spring constant per unit length along the string. Equation 4 also has the same structure as equation 1 if we choose µ(x) and s(x) to satisfy: Equation 5 This relation does not have the physical limitations of equation 3. So the String & Springs apparatus can reproduce quantum wave function shapes even in classically forbidden regions.

Practical matters. Equation 4 is derived in the limit of an infinite number of springs with infinitesimal spacing (along with all of the other simplifications usually made in deriving equation 2) so our first challenge is to attach enough springs close enough together to approximate this limit. Standing waves on a string are also most easily seen at lower frequencies (<100Hz) so our second challenge is to choose the spring and string parameters to keep the resonance frequencies low. Finally, there are no physical solutions to equation 1 in an infinite well if E < V(x) everywhere so µ(x) or s(x) really will have to vary along the length of the string. The first two challenges are somewhat incompatible. To address the first point we need to use small springs very closely spaced. The closer we space the springs the larger the spring constant per unit length. Smaller springs are also more tightly coiled (assuming a constant wire size and type) - which also results in a larger spring constant. To address the second point we need to keep the resonance frequencies low. The angular frequency of just the spring mass system is given by:

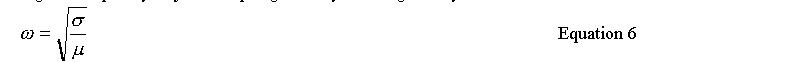
Equation 6 This represents a kind of cutoff frequency between "classically allowed" and "classically forbidden" behavior and can be used to characterize the size of the resonance frequencies since we would like to see standing waves above and below this frequency. The larger spring constants used to address the first point will tend to raise the resonance frequencies of the system rather than lower them. Ultimately we chose the spring parameters to find a happy medium between these two problems and then used a high linear mass density to lower the resonance frequencies. To address the third point, we chose to build apparatus to demonstrate wave function shapes for the two simple potential energy diagrams shown below:

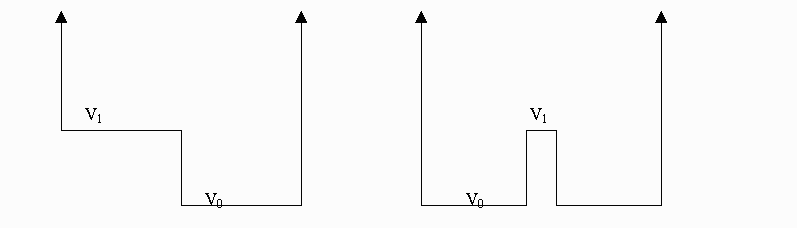
Both of these diagrams represent interesting physical situations and analogs to both are relatively simple to build. We can use a string with constant linear density and springs with identical spring constants and spacing - changing the "potential" by having sections of string with and without springs as represented below:

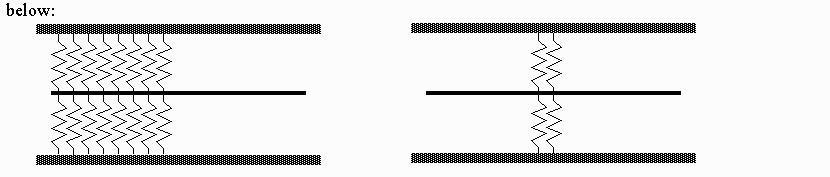
In both cases the ends of the string are fixed to simulate the infinite potential walls. The strings are driven near one end by a mechanical wave generator in order to induce standing waves.

Some Extensions and Limitations By varying the spring constant, spring spacing, and linear density along the whole length of the string we could build, in principle, an apparatus to demonstrate quantum wave function shapes for a whole host of potential energy diagrams. Practically, it would probably be best to stick to piecewise constant potentials with just a few regions. By anchoring a membrane (drumhead) with springs we could build, again in principle, a two-dimensional version of the apparatus. The easiest way to do this may be to use a square grid net with springs at the junctions. Even this would be a lot of work (and a lot of springs)! We have to be careful to remember that this apparatus does not correctly show quantum wave functions - it only shows the shape of the spatial part of stationary state quantum wave functions. The time dependant Schrödinger equation has its time dependence in a first derivative. The time dependant String & Springs equation has its time dependence in a second derivative. This means the dispersion relation is different, the temporal part of the wave function is different, wave pulses travel differently, the spectrum is different, etc… The time dependant String & Springs equation is actually a Klein-Gordon equation - which is the correct relativistic equation for bosons. So Strings & Springs can demonstrate the correct relativistic wave functions of an alpha particle (for example) - time dependence and all.

Results. Prototypes of this apparatus have been built and tested with excellent results. Standing wave shapes and frequencies agree well with theoretic predictions. The apparatus has been demonstrated to students with good results. The springs give a nice visual cue to the extent of the different "potential energy regions" and the wave shapes in those regions nicely show the difference between wave functions in classically allowed and classically forbidden regions. As of the writing of this document the final version of the apparatus, which will be shown at the AAPT meeting, is under construction in our shop - so we do not currently have numerical results from that apparatus. This write-up will be extended to include those results when the final version is complete and tested.

References.

i) See, for example, Griffiths, "Introduction to Quantum Mechanics", Prentice Hall.
ii)See, for example, Symon, "Mechanics", chapter 8, Addison-Wesley.
iii) See Main, "Vibrations and Waves in Physics", Cambridge University Press.