M. J. Moloney
CL-109
Office 812 877 8302
Home
812 466 1328
Revised
11/21/07
Course Materials (Information, Notes, Handouts) Winter 07-08
Contents Projected order of chapters in Meeks, Acoustics.
Tentative allocation of credit
Animation of a pulse reflecting from a boundary
Instructions for adding a slider to a spreadsheet
Driven
damped oscillator spreadsheet
Animation of pulse on a string fixed at
both ends (maple code)
Animation of pulse on a string ; we are
not told the boundary conditions
Driven damped oscillator (graphs, maple
code, problem)
Animation and maple code for simple
vibrating membrane
Transverse waves on rods and bars
(chart, graphs, boundary conditions, maple code)
Elasticity and Bending of Beams
This animation shows a pulse traveling on a string fixed at both ends.

The contents of this maple file are :
strpulse.mws pulse on a string via eigenfunction expansion
Use notation of Meeks, p. 47
An cos n pi ct/L + Bn sin n pi ct/L
An = 2/L integral 0 to L sin n pi x/L y(x,0)
Bn = 2/m pi c integral 0 to L v(x,0) cos n pi x/L
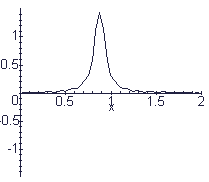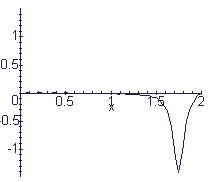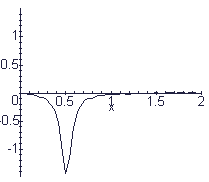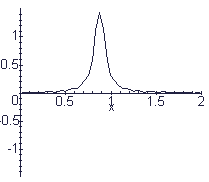
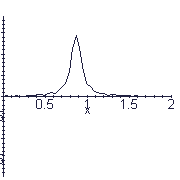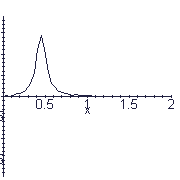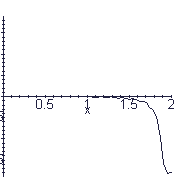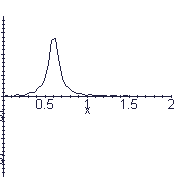
pulse centered at x=7/8 @t=0 pulse isn't really 0 at boundaries,
but close to it.
string from 0 to 2. 11/17/97
restart;with(plots):
c:=4; # pulse speed (which must be string
wave speed!)
y:=3/(2+450*(x-7/8-c*t)^2);
animate(y,x=0..2,t=0..1/2,frames=20,color=black);
# this pulse runs off end of the string!
vy:=subs(t=0,diff(y,t));
N:=30; # of terms in series
L:=2; # length of string
for m from 1 to N do
B[m]:=evalf(2/(m*Pi*c)*Int(vy*sin(m*Pi*x/L),x=0..L));
A[m]:=evalf(2/L* Int(subs(t=0,
y)*sin(m*Pi*x/L),x=0..L));
od:
str:=0:
for m from 1 to N do
str:=str+(A[m]*cos(m*Pi*c*t/L)+B[m]*sin(m*Pi*c*t/L))*sin(m*Pi*x/L);
od: animate(str,x=0..2,t=0..1,frames=30,color=black);
What kind of string is this pulse travelling on? Can you modify the program above to give this behavior?
[This string is not fixed at both ends!]
The response
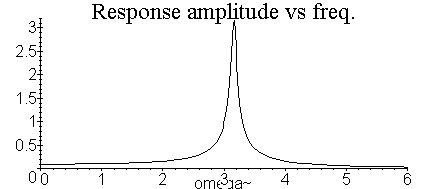
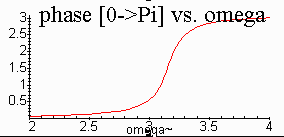
curve
for a driven damped oscillator is shown below, both for
amplitude
vs frequency, and phase vs frequency. The phase shown is the
amount
by which the driver leads the response of
the driven
oscillator.
 |
 |
Click here to download the maple file which generates these graphs. After it comes up, you will want to do a 'Save File', and later open the file in Maple.
The commands in this file are as follows:
drivnosc.mws 9/22/97
Plot the phase and amplitude response of a driven, damped oscillator as a function of frequency.
It is interesting that very heavy damping (b=10, k=10, m=1) crushes the response away from zero frequency.
restart;with(plots):
assume(k,real);assume(m,real);assume(A,real);
assume(omega>0);assume(t,real);assume(b,real);assume(phi,real);
eqn:=A*exp(I*(omega*t+phi))-k*x(t)-b*diff(x(t),t)
= m*diff(x(t),t,t); > s:=dsolve(eqn,x(t));
x:=rhs(s);
values:={A=1,m=1,k=10,b=1/5};
xs:=subs(values,x);
steady:=op(1,xs); #
keep only the oscillating terms for steady state response ev:=evalc(subs(t=0,phi=0,steady));
The conventional phase response is the driver phase - the responding phase, so the amplitude response will be found as exp(-I alph)
assume(alph,real);
cosal:=op(1,ev); sinal:=-op(2,ev)/I;
alph:=arctan(sinal/cosal);
plot(alph+Pi*Heaviside(-alph),omega=2..4,title=`
phase [0->Pi] vs. omega`);
The driver is in phase with the driven system at very low frequencies, and pulls ahead until it is Pi/2 ahead at resonance, and goes on to be Pi ahead (180 degrees out of phase) at very high frequencies.
The Heaviside function forces the inverse tangent to run between 0 and Pi, rather than between -Pi/2 and +Pi/2.
xcc:=subs(I=-I,steady); # get complex
conjugate
xmag:=simplify(steady*xcc); # get magnitude
squared
xev:=simplify(evalc(xmag));
plot(sqrt(xev),omega=0..6,title=`Response
amplitude vs freq.`);
Homework problem P6
a) Figure out the theoretical Q value for the oscillator in the problem above.
b) Re-plot the amplitude response curve in Maple from, say, 3 to 4 sec, and determine the Q 'experimentally' by clicking on the plot at points where the amplitude is 0.707 of the max amplitude. Show your calculations for Q.
c) Double the Q of the system (be sure to
tell
me how you did this). Re-plot and 'experimentally' check that the new
parameters
resulted in the correct value of Q.
Here is an animated vibrating rectangular membrane, in its lowest mode

Click here to download the maple file which does this animation. Do a 'Save File', then open the file in Maple.
Here is the code in the maple file:
restart;with(plots):
Lx:=2; Ly:=1;
g:=sin(Pi*x/Lx)*sin(Pi*y/Ly);
plot3d(g,x=0..Lx,y=0..Ly);
c:=100; # wave speed on membrane
omega:=c*sqrt((Pi/Lx)^2+(Pi/Ly)^2);
# lowest mode angular freq
Nframes:=10; tfac:=2*Pi/(omega*Nframes);
for i from 0 to Nframes-1 do
plt.(i):=plot3d(sin(omega*i*tfac)*g,x=0..Lx,y=0..Ly);od:
display([plt.(0..Nframes-1)],insequence=true);
#
this is the animation
Transverse waves on bars and rods.
They are solutions of y'''' = k^4 y = w^2 /(kap^2 c^2),
where c = sqrt(Y/rho), and kap = sqrt(int r^2 dA/ int dA).
frequencies: w = k^2 kap c.
same frequencies for free-free and clamped-clamped bars, but
different
functions!
| free-free bar
y''( +/- L/2)=0 y'''( +/- L/2)=0 |
clamped-clamped
y( +/- L/2) = 0 y'( +/- L/2)=0 |
clamped-free
y(0)=0=y'(0) y''(L)=0=y'''(L) |
| even:
solve tan kL/2 = -tanh kL/2 kL =. 3, 7, 11, etc. Pi/2 |
even:
solve tan kL/2 = -tanh kL/2 kL =. 3, 7, 11, etc Pi/2 |
all solutions : solve
cos kL cosh kL = -1 |
| odd
solve tan kL/2 = +tanh kL/2 kL = . 5, 9, 13, etc. Pi/2 |
odd
solve tan kL/2 = +tanh kL/2 kL = . 5, 9, 13, etc. Pi/2 |
kL =. 1, 3, 5, 7, etc Pi/2 |
| lowest even mode
|
lowest even mode
|
lowest mode
|
| lowest odd mode
|
lowest odd mode
|
next-lowest mode
|
Here is the maple file which produced the graphs shown above. Do a 'Save File, then open later in Maple
Some theory on beam bending. .

Examine the neglect of Ic alpha in the derivation of equation [2] above, and then obtain an improved equation for the bar, which enables us to make frequency corrections at high frequencies.

Vibration frequencies and equations - free-free, clamped-clamped, and clamped-free.