A simple source of acoustic radiation is predicted to radiate twice as much power very close to a large rigid wall as in free space. This is because the sound bouncing off the wall interferes with the sound directly radiated (we could say there is an 'image' of the source behind the wall). This doubles the amplitude. Because the intensity depends on the square of the amplitude, the intensity is quadrupled. Next to the wall, we are radiating into only half the available space, so the total power comes out doubled over what the simple source would radiate in free space.

I spent well over a year trying to see this effect clearly using the Q of a cylindrical pipe open at one end and closed at the other. The results were interesting, but they were not altogether right.

Then I got the idea of using a wooden resonator box with a tuning fork. This has a very high Q, and the sound lasts a long time before decaying away. I would measure it a varying distances from a large wall to see if it gave the right effect.

When I took 10 seconds of data on the decaying wave, I was able to fit the 10000 data points quite accurately to the equation of a decaying oscillator.

From this fit I got the 'decay constant' b . Then I could calculate Q from

Q = w /(2b ) = p f/b .

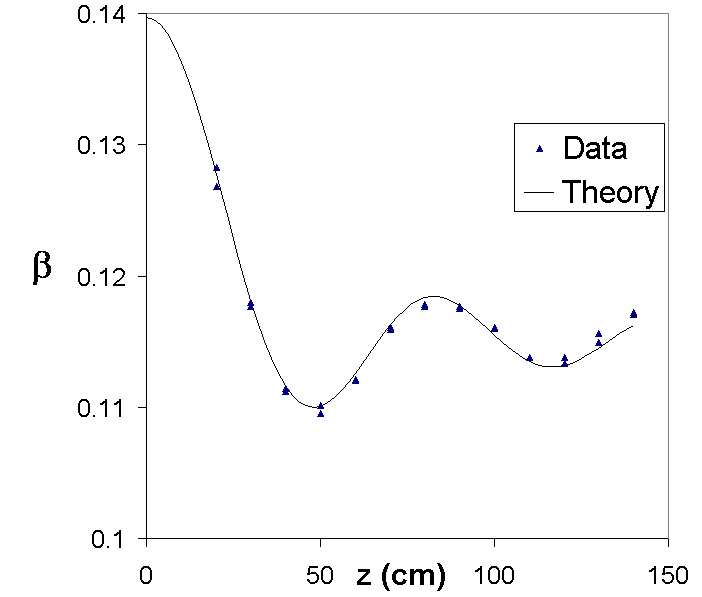
I measured Q for resonator tuning fork box at a number of distances from a large wall in BL-114 after fall classes were over in November 2002. The theory predicts that the radiated power near a large wall should behave in an oscillatory way. The decay constant b contains the energy losses from the system, so it should have some constant loss from the wooden box, and also a varying loss from the sound radiated near the wall.

Since b contains the radiative losses, I plotted b vs. distance from the wall. This agreed very nicely with the theory.

This work has been published in the August 2003 issue of the American Journal of Physics.
(Simple acoustic source radiation near a large wall, Michael J. Moloney, Am. J. Phys., 71,794 (2003)).