
Supported by NSF grants DMS-0097804, DMS-0352940, DMS-0647121, DMS-1003924


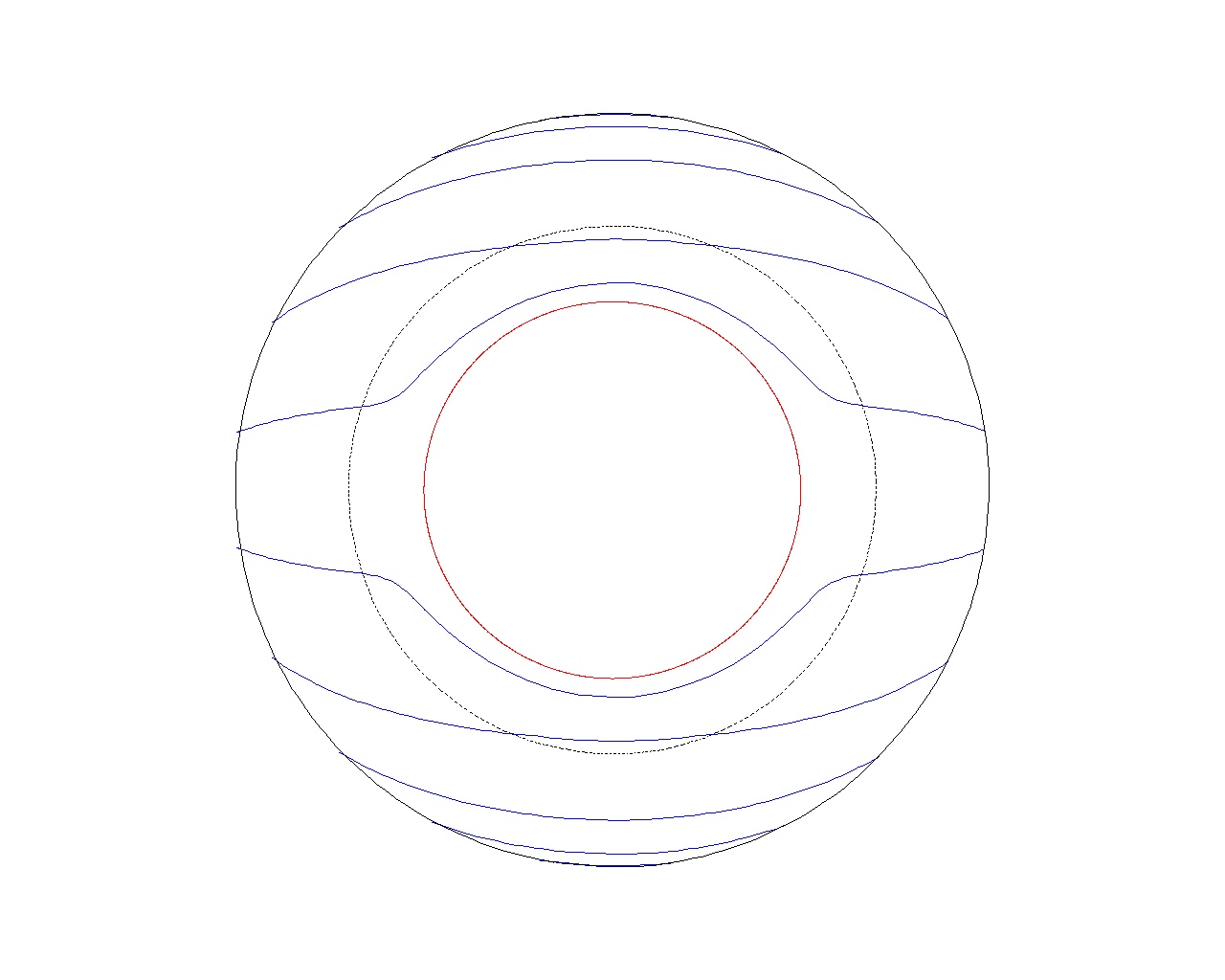
Above: Effect of a crack on the electric potential (left), cloaking against thermal energy (right).
In the study of differential equations (ordinary or partial) the usual procedure is to find the solution to a given differential equation with some initial and/or boundary conditions. In "Inverse Problems" the situation is reversed: one is given the solution (or some information about the solution) to an "unknown" differential equation and then must determine the differential equation. These kinds of problems come up frequently in the field of non-destructive testing or medical imaging, in which one seeks to image the interior of an object without damaging the object. To do this, some kind of energy---electromagnetic, thermal, or mechanical---is applied to the boundary of the object. The energy flows through the object in a quantifiable way that depends on the interior structure. By taking boundary measurements of the object's physical response, one tries to deduce the interior structure of the object. The flow of energy is generally governed by a partial differential equation (PDE), and the interior structure of the object is manifest as unknown coefficients or boundary conditions in the PDE.
As a specific example, consider imaging the interior of an object using heat. A known heat flux is applied to the outer boundary of the object. The heat flows through the interior and the temperature of the outer boundary is monitored over time. If there are defects in the object---say cracks or holes---the flow of heat in the interior is altered, and this (we hope) manifests its presence in the boundary temperature measurements. The trick is to take these temperature measurements and recover the location of the crack or hole, if present. The flow of heat through the object is governed by the heat equation, a partial differential equation, and the defect can be modeled as an unknown interior "boundary", with some unknown boundary condition.
The same type of imaging can also be done using electrical current, mechanical vibration, or other types of excitation.
A closely related area to inverse problems is the recent hot topic of "cloaking and invisibility". I've had a few students work on problems in this area.
The REU Inverse Problems group in the summer of 2002 worked on inverse problems involving the imaging of cracks using thermal and electrical methods. The usual model of a "crack" assumes that the crack blocks the flow of thermal or electrical energy (see the figure on the right above, in which the flow is forced to go around the crack). We considered the problem of locating a crack in a thermal or electrical conductor in which the crack does not completely block the flow of energy, but merely presents an impedance to the flow. The goal is to find the crack location and identify the function that governs the impedance of the heat flow. The students obtained original publishable results.
The work is a blend of mathematical modeling, theory related to partial differential equations, and numerical analysis.
Sameer Shah (MIT) and Cynthia Gangi (Eckerd College) considered a one-space-variable time-dependent version of the problem and obtained nice results concerning the problem of locating the crack and impedance function, with a computational algorithm. See Rose-Hulman Mathematics Technical report " Characterizing a Defect in a One-Dimensional Bar", MSTR-0201.
Ron Ogborne (SUNY Fredonia) and Melissa Vellela (Boston University) extended some previous results of Andriex and Ben Abda, concerning the identification of linear cracks from steady-state heat (or electrical) measurements, and produced a nice algorithm for locating cracks and identifying the impedance function. This work in the journal "Inverse Problems", February 2005. Here's a preprint of the original tech report, A Thermal Imaging Approach for Finding a Generalized Linear Crack ", MSTR-0202. A version of this paper appeared in the journal Inverse Problems in February 2005.
The group this last summer worked on two different inverse problems. The first concerns imaging the shape of the interior wall of a blast furnace by using only temperature and flux measurements from the exterior wall (since the interior is a rather harsh environment!) The trick is that the interior wall profile may actually change shape over time, either due to the corrosive nature of the interior (makes the wall thinner) or the build up of deposits (makes the wall thicker). From a practical point of view, one doesn't want the wall to get too thick, and too thin is also an obvious danger. This is a problem I've discussed with Tom Fredman at Abo Akademi University in Finland.
Holly Walrath and Natasha Yarlikina considered a simplified version of the problem, to gain insight into the nature of the mathematical difficulties: They consider a one-dimensional bar, one end at x=0, the other end moving in time with end at x=L(t) for some unknown function L(t). The interior of the bar has temperature u(t,x) at time t, position x, where u satisfies the heat equation. The goal is to use measurements of u(t,0) and u_x(t,0) (at the accessible end of the bar, like the outside of the furnace) to determine the function L(t) (knowing, for example, that u(t,L(t))=A for some known constant "A"). They came up with a couple of different approaches for solving this problem, each with different strengths and weaknesses. and identifying the impedance function. Here's a preprint of their paper, Determining the Length of a One Dimensional Bar with Thermal Measurements .
Nic Trainor and Rachel Krieger considered a beautiful new approach for locating multiple perfectly-insulating linear cracks inside a thermal (steady-state) or electrical conductor using boundary measurements. The algorithm makes clever use of Green's third identity and a new Lemma concerning how the lengths of the cracks manifest themselves in the boundary data. This work is a beautiful illustration of how some mathematical analysis can make a hard computational problem much easier and faster. They also derived results on what type of input fluxes give optimal resolution. Here is a preprint of the paper, Fast Reconstruction of Cracks Using Electrical Boundary Measurements , a version of which appeared in the Journal of Computational and Applied Mathematics in March 2007.
This summer again the students chose to pair up. Nic Christian and Mat Johnson considered the following problem, analogous to that considered by Ron and Melissa in 2002: Consider a 2D region or "object" Omega which contains an inclusion or subregion "D" (possibly with different but known physical properties than Omega). Suppose the boundary of D should be bonded firmly to the surrounding material but may have corroded or disbonded. We want to be able to detect such damage from the exterior of Omega, using either thermal or electrical imaging. Like the 2002 crack problem, we assume that the damage manifests itself as a kind of "contact resistance" on the boundary of D. This contact resistance may vary from point to point on the boundary of D, and our goal is to recover this resistance function from Cauchy data for the steady-state heat (Laplace's) equation. The motivation for this problem comes from NDE for composite materials, in which D represents a deliberately included object, part of the composite "matrix", which may suffer from disbonding. Mat and Nic came up with a nice scheme for constructively recovering the "disbond" function on the boundary of D, did a thorough analysis of the ill-posedness of the problem, and devised an effective and efficient regularization scheme, with many numerical examples. Here's a preprint of their paper, Nondestructive Testing of Thermal Resistances for a Single Inclusion in a Two-Dimensional Domain.
Janine and Dave worked on generalizing the results of Nic and Rachel on finding multiple cracks in an object from the summer of 2003 to the case in which the cracks do not completely block the flow of heat (or electrical current) but instead allow some heat flux over the crack, according to the constitutive law du/dn = k[u], in which du/dn is the normal derivative of the temperature on a crack and [u] is the temperature jump over the crack. Here "k" is a constant that governs the "resistance" presented by the cracks. The were indeed able to generalize the results, using a new and somewhat simpler approach. Here's a preprint of their paper, Reconstruction of Partially Conductive Cracks Using Boundary Data . A version of this paper appeared in the journal Inverse Problems in 2006.
This summer students Don Brown and Mark Hubenthal paired up to consider the problem of locating one or more circular inclusions ("holes") inside a region by using the fully time-dependent heat equation. Specifically, we pump heat energy into the boundary of the object (typically the heat "turns off" after a short time) then measure the boundary temperature response for some time interval. They found a couple different approaches for locating the inclusions, one which works for multiple inclusions (but has certain limitations or assumptions on the nature of the input flux) and another approach which is more flexible, but works only for a single inclusion. Both work beautifully on numerical data, and are very fast. Here's a preprint of their paper, Time Dependent Thermal Imaging of Circular Inclusions. A nice challenge for next year would be a method for finding multiple inclusions using the latter algorithm, as well as an analysis of what types in input flux give optimal resolution.
Hilary and Shannon worked on generalizing the results of Mat and Nick from last year, concerning the problem of locating inclusions which are not holes, but rather in which the inclusions have an interface to the rest of the domain which manifests itself as a kind of contact resistance to the flow of heat (see the above description of the analogous problem for cracks from 2004). This resistance is quantified by the constitutive law du/dn = k[u], in which du/dn is the normal derivative of the temperature on an inclusion and [u] is the temperature jump over the inclusion boundary. Here "k" is a known constant that governs the "resistance" to heat flow. the cracks. The were indeed able to generalize the previous results, by adapting ideas from the work of Janine and Dave from summer 2004, and come up with a delightfully simple and fast algorithm for find many such blobs using steady-state thermal data (or electrical impedance data). Here's a preprint of their paper, Thermal Imaging of Circular Inclusions Within a Two-Dimensional Region.
This summer students Tom Werne and James Preciado considered the problem of locating one or more circular inclusions ("holes") inside a region by using the fully time-dependent heat equation, the same problem considered last year by Don and Mark, but with an attempt to remove certain restrictions on the input flux and truly deal with the transient nature of the problem. They found two very different approaches for locating the inclusions. One is based on certain symmetries in the data when a single circular inclusion is present. It's simple, but works only for a single inclusion. The second approach is based on a time-dependent version of the "reciprocity gap" approach, and works for multiple inclusions. However, certain approximations that were made are not fully justified and could probably be improved. Nonetheless, both work well on numerical data, and are fast. Here's a preprint of their paper, Utilizing Thermal Testing for Recovering Voids in Two-Dimensional Regions.
Breeanne and Victor looked at generalizing the reciprocity gap approach of previous years to the full three dimensional case (for steady-state imaging), with slightly different approaches. Breeanne used certain singular test functions (based on the Green's function for the Laplacian in 3D) to show how one can extract the center and radius of a single spherical inclusion in an object, and illustrated the approach with some numerical examples. Victor used the reciprocity gap method with certain exponential test functions to show how one can recover the center and radius of one or MULTIPLE spherical inclusions. Again, the method worked successfully (and rapidly) on simulated data. In all cases it was assumed that the inclusion completely blocks heat/electrical flow, though Victor did some analysis for the case du/dn = k[u], similar to the work of summer 2004. Here's a preprint of Breanne's paper, Thermal Imaging to Recover a Defect in Two or Three-Dimensional Objects and Victor's paper, Nondestructive Recovery of Voids within a Three-Dimensional Domain using Thermal Imaging.
Students Esther Chiew and Vincent Selhorst-Jones considered some inverse problems on a rectangular network of resistors (a discrete approximation to the inverse problem for electrical conductivity.) Inverse problems on resistor networks have been studied for many years at the University of Washington REU program. One has a two-dimensional grid of resistors (in our case, a rectangular grid); the boundary or exterior resistors are accessible. A current is injected into one or more of these boundary resistors and then the resulting voltage is measured on some portion of the boundary. From this one attempts to determine the resistance of the interior resistors, or perhaps the condition of some other inaccessible part of the resistor network. Esther and Vincent considered the possibility of finding either "back surface corrosion'' or interior voids (missing resistors) in a network using this approach. The problem is quite unstable, so they also developed insightful regularization techniques to stabilize the process. Here's a preprint of their paper, Determining the Shape of a Resistor Grid Through Boundary Measurements.
David Kiblinger and Michael Janas considered an inverse problem in "electrothermal imaging" (a technique which seems to be little-explored, in both the experimental and mathematical community). One injects an electrical current into an object. This induces interior Joule heating that depends on the applied current pattern, and of course the interior condition of the object. One then measures the boundary temperature of the object and tries to use this information to determine the interior electrical and/or thermal properties of the object. The forward problem consists of Laplace's equation (or some variation thereof) coupled to the heat equation. David and Michael considered the problem in both one and two-dimensional versions, in which the object has variable electrical conductivity but uniform thermal properties. In one dimension they developed effective methods for imaging the conductivity from thermal data, as well as finding "localized" interior defects. Considerable progress was made on a linearized version of the problem in two dimensions as well, but much work remains to be done. Here's a preprint of their paper, Electrothermal Imaging in One and Two Dimensions.
Court Hoang and Kate Osenbach considered a problem similar to that of Vincent and Esther, that of recovering "back surface" corrosion in a two-dimensional object from electrical measurements on an accessible portion of the outer boundary, but with general boundary conditions on the corroded portion of the surface. The same techniques would extend to three-dimensions. The intent was to then to apply the same techniques to analyze how this corrosion can be imaged using electro-thermal techniques (by measuring the temperature profile induced by an injected electrical current) but they didn't get quite that far. Here's a preprint of their paper, Electrical Impedance Imaging of Corrosion on a Partially Accessible Two-Dimensional Region.
Brooke Phillips and Tess Anderson consider a couple of questions related to "cloaking", that is, making an object appear invisible to an observer that tries to image the object with electromagnetic energy. In this case, they supposed the observer uses impedance imaging. They showed how the same "change of variables" technique often used in cloaking can be adapted to instead disguise an object, that is, make the object appear to be something else (larger, rotated, a different shape, etc.) They then consider the problem of cloaking an object in the context of thermal imaging, in which the flow of energy is governed by the heat equation (steady-state, in this case). Here's a preprint of their paper, Anti-cloaking: The Mathematics of Disguise.
Brittany Ambeau, Harris Enniss, and Stefan Schnake considered an electrothermal version of the back-surface corrosion problem, and so extended some ideas from 2009. Specifically, we impose a current flux on some accessible portion of the boundary of an object which may have some kind of damage to its boundary, in an inaccessible area. The current induces internal ohmic heating, and since the current is perturbed by the corrosion, so is the heat that's generated. We then observe the temperature on some accessible portion of the boundary and try to infer the corrosion profile. They found that this is in fact possible, and indeed can be done more stably than with just electrical measurements alone. It's a nice example of the "multimodal" imaging approach many people are now considering for inverse problems. Their report is Nondestructive Electrothermal Detection of Corrosion.
Maple So took the ideas in the paper "Impedance Imaging, Inverse Problems, and Harry Potter's Cloak" by Tanya Leise and me and extended them to work in the context of the periodic heat equation. She found that if the input heat flux to the region is periodic of the form exp(i*omega*t)*g(x,y) for some input flux g then the same general change-of-variables approach works to cloak an object, and the cloak needed does not depend on the frequency (the estimates concerning the efficacy of the cloak do, however). Her report is Cloaking Against Thermal Imaging
Chase Mathison and Laura Booton analyzed an electromagnetic inverse problem in which ones want to determine the properties in each layer of a metallic multi-layered structure. This information is to be deduced by placing an electromagnetic coil near the sample. The coil can be driven at a variety of frequencies and the data collected consists of impedance measurements at each frequency. From this we want to find layer thicknesses, conductivities, permeabilities. They analyzed the specific case of a single layer structure consisting of an infinite slab of material with unknown properties. Here is a copy of their report, Determining Properties of Metal by Analyzing Changes in Impedance.
Many questions concerning theory, computation, and modeling remain unanswered. Among those raised, but not answered, by last summer's participants:
Kurt Bryan, Department of Mathematics, Rose-Hulman Institute of Technology, Terre Haute IN 47803.
Phone: (812) 877-8485
email: kurt.bryan@rose-hulman.edu