J-Tests: To Nest Or Not To Nest, That Is The Question
I. INTRODUCTION
Allegations of specification errors can be a kiss of death for applied econometricians. Accusations of specification errors are easily made and innocence is often hard to prove, especially when economic theory is inconclusive. Specification errors are serious because if a regression model omits relevant explanatory variables or if it uses the wrong functional form, its estimates are biased and inconsistent. Equally troubling, if a misspecified model is used for hypotheses testing and statistical inference, misleading results may occur. Statistical specification tests may detect a specification error or they may show that fears of misspecification are groundless. This paper looks at two specification tests - - Davidson and MacKinnon’s (1981) non-nested J test and the nested, hybrid model specification test.
The J test is commonly used in the literature. According to the Social Science Citation Index, the Davidson and MacKinnon paper that introduced the J test has been cited in 497 separate articles between 1984 and 2004.[1] Another sign of the increased acceptance of using J tests in econometric practice is the number of textbooks that discuss this specification test.[2] Some textbooks cite reasons why the J test is superior to the nested specification test. However, this paper shows there is a special case when the non-nested J test and the nested test give identical answers.
Choosing Between Two Competing
Specifications
Both
the non-nested J test and the nested specification test can be used when there
is a choice between two competing model specifications. Suppose that both Model A and Model B are
theoretically plausible in describing the behavior of an endogenous
variable. Model A states that
while the model specification Model B, which is also theoretically possible, is
In models specified in equations
(1) and (2), there are N observations, and both Models A and B have the same
dependent variable, y. Referring to
Model A, each observation i (i = 1, …, N) has k + m explanatory variables (xji,
j = 1, … , k, and wji, j = 1, … , m) and there are m + k +1
regression parameters (
) including the intercept (
). On the other hand,
Model B has k + n explanatory variables (xji, j = 1, …, k, and zji,
j = 1, … , n ). Including the intercept
(
), Model B has k + n + 1 unknown regression parameters (
i, i = 0, …, k, and 
i, i = 1, …, n).
Both models can have the same subset of explanatory variables. For every observation, both Models A and B in the above equations include the same k explanatory variables, xj, j = 1, …, k. However, because theory is inconclusive on what other explanatory variables belong in the model, Model A includes m more explanatory variables, wj (j = 1, …, m), while Model B includes a different set of n explanatory variables, zj, j = 1, …, n. While each of these different subsets of explanatory variables are unique, each set is theoretically plausible, resulting in uncertainty over which model is the correct model specification.
The First Specification Test: The Non-Nested J Test
Ways
to empirically determine the correct model specification include performing a
nested specification test and a non-nested J test. Table 1 reviews the necessary steps to
perform the non-nested J-Test. As Table
1 shows, the J test requires estimating four different regression equations. In Step 1, Model A is estimated and the
predicted values of the dependent variable, 
, are obtained. Step 2
is analogous to Step 1 in that Model B is estimated and the predicted values
from this model, 
, are also derived. In
Step 3, the predicted values from Model B are included as an explanatory
variable in Model A, while the predicted values from Model A are included in
Model B’s specification in Step 4. The critical
idea is whether the predicted values from one model add significant explanatory
power to the other model.
As Table 1 indicates, the non-nested J test has four possible outcomes. Two of the outcomes give definitive results regarding the best specification of the model, but the other two outcomes yield inconclusive results. First, the non-nested J test may fail to reject Model A while simultaneously rejecting Model B. Second, the converse may happen where Model B is not rejected but Model A is rejected. In these cases, the predicted values of the superior model are statistically significant when added as an additional explanatory variable to the specification of the rejected model. However, when the predicted values from the rejected model are included as another explanatory variable in the superior model, the regression slope coefficient associated with the predicted values is not statistically different from zero. The inconclusive results occur when either the J test simultaneously rejects or fails to reject both models.
The Other Specification Test: The Nested Test
While the non-nested J test requires estimation of four different regressions, the nested specification test requires the estimation of two regressions. The nested specification test is essentially an F test which determines whether several slope parameters are simultaneously equal to zero. Table 2 lists the steps for this nested test.
As indicated in Table 2, this statistical test requires the estimation of two regressions. First, Model A is estimated, and then a hybrid or nested model that includes all the explanatory variables in Models A and B is estimated. Regarding the nested model, attention is directed towards the slope coefficients of those explanatory variables that are in Model B and not included in Model A. The null hypothesis is that all these slope coefficients are simultaneously equal to zero. If this nested F test fails to reject this null hypothesis, then the exogenous variables that are unique to Model B offer no additional explanatory power, and Model A is chosen over Model B. If the null hypothesis is rejected, then the variables that are unique to Model B add important explanatory power to Model A, indicating that Model A might be incorrectly specified.
Which Specification Test Is Best?
In terms of application, the nested, hybrid specification test might be preferred to the non-nested J test because it requires estimation of only two rather than four regressions. Another problem is the possibility that the J test might yield inconclusive results. Finally, the J test is a large sample test where the critical test statistic has the proper statistical distribution only asymptotically. Gujarati (2003, p. 534) notes that in small samples “the J test may not be very powerful . . . because it tends to reject the true hypothesis or model more frequently than it ought to.”
However, the nested, hybrid specification test also has its problems. With the inclusion of every possible explanatory variable, Fomby, Hill, and Johnson (1984, p.416) note that “multicollinearity problems are a distinct possibility with the coefficients being imprecisely estimated.” Gujarati (2003, p. 531) states that “the artificially nested model . . . may not have any economic meaning.” There is a chance that the hybrid model generates asymmetric results depending on the choice of the reference model. Model A was the reference model in Table 2 because the statistical test investigated whether the variables unique to Model B added any explanatory power to Model A. Conversely, Model B could have been chosen as the reference model and then the hybrid model could have been used to test whether those exogenous variables that are unique to Model A add any statistically significant explanatory power to Model B. Fomby, Hill, and Johnson (1984, p. 416) conclude that
The choice of the reference model could determine the outcome of the choice of the model. Thus, though the mechanical nesting procedure has great appeal, it does incur statistical problems.
However, this paper shows that there is a special case when the non-nested J test and the nested, hybrid specification test give equivalent results. This case occurs when there is debate over the inclusion of only one independent variable. Assume that both Model A and Model B agree on including the same subset of explanatory variables. Both models assume there are k explanatory variables and the first k – 1 explanatory variables in both models are identical. However, disagreement occurs over the kth exogenous variable, the last exogenous variable included in the model. Model A assumes the last explanatory variable is variable w, while Model B assumes the last explanatory variable is z. This paper shows that when there is only debate over one exogenous variable, either w or z, the non-nested J test and the nested, hybrid model test give identical results. In this case, the nested, hybrid specification test may be preferred as it reveals all the same information while running three less regressions.
The next section of the paper provides a simple, empirical example showing a case where the two specification tests give equivalent results. The paper’s third section introduces the two models and the notation. The paper’s fourth section lists three propositions about the statistical properties of this special case and uses matrix algebra to prove the first proposition, which is the main result. A summary and concluding thoughts are in the fifth and final section of the paper.
II. A NUMERICAL EXAMPLE
To illustrate a case where both the non-nested J test and the nested, hybrid specification test give the same answers, the following section uses a simple, empirical model of the Phillip’s curve to motivate the discussion. The empirical results presented here are not novel or path-breaking. Though the model and its empirical results add nothing to the literature, the intent of this section is to show an empirical example of a case where both specification tests yield test statistics with the same absolute value.
The Correct Functional Form for the Phillip’s Curve
The simple Phillip’s curve examines the short-run trade-off between inflation (π) and unemployment (U). Usually there is an inverse relationship between these two variables, and in the past, policy makers have taken steps to reduce unemployment while accepting the short-run cost of higher inflation. Suppose two different, but both theoretically plausible, empirical models of the Phillip’s curve are proposed. While the correct functional form is uncertain, assume that current inflation in time t (πt) is a function of two variables: inflation in the previous period (πt-1) and current unemployment (Ut).
The specification for the first model, Model A, is
and Model B’s specification is
The difference in the specification
of the two models is easy to spot. In
Model A, current unemployment (Ut) enters the specification linearly
while the same variable enters the specification in Model B in a reciprocal
fashion (
). Since inflation is
a time series exhibiting some inertia, both β1 and α1
are expected to be positive. If there is
an inverse, short-run relationship between current inflation and current
unemployment, then β2 is expected to be negative while α2
should be positive.
The Two Specification Tests
To
determine the best model specification with the correct functional form, the
J-test requires the estimation of the models listed in equations (3) and
(4). Let the predicted values of
inflation from Models A and B be denoted as 
and 
, respectively.
Performing the J test requires including the predicted values from Model
A as an additional explanatory variable in Model B and the predicted values
from Model B are also included as an additional right-side variable in the
specification of Model A. After estimating
the two models in equations (3) and (4), the J test requires the estimation of
still two more additional equations:
and
The outcome of the J test rests on the statistical significance of the ordinary least squares (OLS) estimates of δ3 and γ3. In the search for the proper functional form, hopefully only one of these estimates is statistically different from zero while the other estimate is not. The J test will be inconclusive if both of these estimates are either simultaneously statistically different from zero or not.
To perform the other specification test using the nested, hybrid model, the following regression is estimated
Here the choice between Model A and
Model B depends on the statistical significance of the estimates of 
and 
. A definitive choice
between the two models can be made when one of these estimates is statistically
different from zero and the other estimate is statistically insignificant. Like the J test, choice of the proper
functional form becomes more complicated when the nested specification test
yields inconclusive results when and are both
simultaneously statistically different from zero or both simultaneously
statistically insignificant.
The Data and the Empirical Results
The estimation results for all the regressions described in equations (3) through (7) are listed in Table 3. Both the consumer price index (CPI) data and the unemployment rate data are from the Bureau of Labor Statistics. The annual inflation rate was derived from the CPI data for all urban consumers (1967 = 100) and the unemployment rate is the seasonally unadjusted value reported for those unemployed workers who are 16 years of age or older.[3] Annual observations of these variables are available from 1949 to 2003. Since the Chow test indicates there is parameter instability at the breakpoint of 1974, the regressions in Table 3 are based on the 30 annual observations between 1974 and 2003.[4]
Looking at the estimation results for Models A and B in Table 3, all the estimated slope coefficients are statistically significant at the 10 percent level or better and the coefficients have the expected signs. The models have adequate explanatory power as the R2 is either 71 or 75 percent. Even though the data set consists of annual time series, neither regression appears to be plagued by serial correlation. In the case of Model A, the Breusch-Godfrey serial correlation test indicates there is no first-order autocorrelation with an insignificant F statistic of 1.25 and a p-value of 0.27. Nor is first-order autocorrelation present in Model B as the Breusch-Godfrey autocorrelation test has an insignificant F statistic of 2.34 with a p-value of 0.14.
Determining The Correct Functional Form
While both models have significant slope coefficients with correct sign and other desirable statistical results, the specification tests reported in Table 3 indicate that Model A is the superior model. First refer to the J test results reported in column labeled “Test 1.” The null hypothesis that the coefficient associated with the predicted values from Model B is equal to zero cannot be rejected at the one percent level of significance. Therefore, the predicted values of inflation from Model B fail to add any meaningful explanatory power to Model A, indicating the superiority of Model A’s specification. On the other hand, referring to the column labeled “Test 2” in Table 3, the hypothesis that the predicted values of inflation from Model A fail to add any explanatory power to Model B is rejected at the 1 percent level. Since the predicted values of Model A improve the performance of Model B, and the converse is not true, given a relatively strict level of significance set at one percent, the J tests indicate that Model B should be rejected in favor of Model A.
The nested specification test agrees with the results of the J test. Referring to the column labeled “Test 3,” the coefficient associated with the unemployment rate equals -2.32 and it is statistically different from zero at the 1 percent level. But the coefficient associated with the reciprocal of the unemployment rate equals -58.63, which is statistically different from zero only at the 10 percent level. Given a stringent significance level equal to one percent, then the conclusion is that the unemployment rate enters the model specification in a linear fashion rather than as a reciprocal.
The t statistics from both specification tests have the same absolute
value
The purpose of the empirical example reported in Table 3 is to show how the J test and the nested, hybrid model specification test yield the same results when the two models in question differ by only one variable. Referring to Table 3, examine the three columns labeled “Test 1,” “Test 2” and “Test 3.” Looking at the “Test 1” column, when the predicted values of Model B are included as another explanatory variable in Model A, the t statistic associated with the coefficient is equal to -1.98. This is exactly the same t statistic associated with the reciprocal of the unemployment rate in the nested specification test reported in the column labeled “Test 3.” Likewise, the absolute value of the t statistic associated with the predicted values of Model A in the “Test 2” column and the absolute value of the t statistic accompanying the linear unemployment rate in the “Test 3” column are exactly the same value, 2.92.
Based on this example, the generalization becomes when two model specifications differ by one variable, the nested specification test and the J test produce the same results as the test statistics have the same absolute values. In the nested, hybrid model, the absolute value of the t statistic of one of the exogenous variables in question equals the absolute value of the t statistic of the predicted values from that variable’s model in the J test. This result will be proven in the fourth section of the paper. When two models differ only by one variable, one can save time performing specification tests. The single nested, hybrid model, obtained by running only one regression, will obtain the exact same results of the J test without having to estimate the four regressions needed to perform such a test.
The explanatory variables in both tests have the same slope
coefficients
The
estimated slope coefficient for the linear unemployment rate in the regression
performing the J test in the “Test 1” column has the same value as the slope
coefficient of the linear unemployment rate in the hybrid model in the “Test 3”
column. Both of these coefficients equal
-2.32. Analogously, the slope
coefficient associated with the reciprocal of the unemployment rate equals
-58.63 in the columns labeled as “Test 2” and “Test 3.” Since these coefficients have the same
standard errors, the simple t statistic testing whether the coefficients are equal
to zero are also identical. The
generalization is that when comparing the non-nested J test with the nested
specification test, the coefficients, standard errors, and t statistics
associated with a given explanatory variable are the same in both regressions.
Both tests have identical regression diagnostic statistics
It is also noteworthy that other diagnostic regression statistics of the two J test regressions and the nested, hybrid model are also identical. For example, the R2s, the adjusted R2s, the F test statistics, the Durbin-Watson tests, and the rest of the other statistics reported in the bottom half of Table 3 are the same in the columns labeled “Test 1,” “Test 2” and “Test 3.” Table 3 also hints why these results occur. Examining the last three columns in Table 3, all these three regressions have the identical residual sum of squares, 65.36. Based on this result, one can infer that the regressions reported in the last three columns of Table 3 have identical residuals for a given observation.
III. MODEL SPECIFICATION: NULL AND ALTERNATIVE HYPOTHESES
Suppose a researcher has to choose between two competing model specifications and economic theory is inconclusive on which model specification is correct. The key assumption is that the two specifications differ only in the choice of one explanatory variable. The first model specification, the null hypothesis, is
while the competing model specification or the alternative hypothesis is
Given N observations, y is the N x 1 vector of observations on the dependent variable. The N x 1 vector of residuals under the null hypothesis is e0, while eA is the corresponding N x 1 vector of residuals under the alternative hypothesis.
Referring
to equation (8), the explanatory variables under the null hypothesis are found
in matrix X0 with a dimension
of N x (k+1). Likewise, the N x (k+1)
data matrix under the alternative hypothesis is XA. The first
column of both X0 and XA is a vector of ones
because both models include an intercept.
The vector of unknown regression parameters under the null hypothesis is
and, under the
alternative hypothesis, 
is the vector of
unknown parameters to be estimated. Both
and are dimensioned (k+1) x
1, and the first element in each vector is the intercept.
As equations (8) and (9) indicate, if both X0 and XA are partitioned into a submatrix consisting of the first k columns and a vector consisting of the last column, they both have a common submatix, X, which is dimensioned N x k. This follows from the assumptions that, under the null or the alternative hypotheses, the first k – 1 explanatory variables in both models are the same. The first column of X consists of a vector of ones because an intercept is included in both models and the remaining k – 1 columns of X are vectors of the observations on the explanatory variables that both models have in common.
Finally, equations (8) and (9) highlight the critical difference between the model’s specification under the null and alternative hypotheses. While the first k – 1 explanatory variables in both model specifications are the same, the models differ over the selection of the last, kth explanatory variable. Under the null hypothesis, the last explanatory variable consists of the observations in vector w, while vector z captures a different explanatory variable under the alternative hypothesis. Vector w has a dimension of N x 1, and it is the last column of X0, the data matrix under the null hypothesis. However, the last column in XA, the data matrix associated with the alternative hypothesis, consists of the vector z which is also N x 1.
Given
the null hypothesis, the vector of the OLS estimates is 
where 
is a
(k + 1) x 1 column vector. Likewise, under the alternative hypothesis,
the (k + 1) x 1 vector of OLS estimates is 
.
Model Specification Tests
To
help determine the correct model specification, two statistical tests can be
performed. The first statistical test
consists of estimating a nested model that includes both of the variables being
considered, w and z, as explanatory variables. Performing the nested test involves
estimating a single regression equation. The second procedure, Davidson and
MacKinnon’s J test, is a non-nested statistical test that involves estimating four
different regression models.
The nested hypothesis test
The regression testing the nested hypothesis is
where λ
is a k x 1 vector of regression parameters to be estimated. This vector includes the intercept and the
slope coefficients for the k – 1 explanatory variables that are common in both
models. Additional regression slope
parameters include both 
and which are 1 x 1
scalars that need to be estimated.
Finally, eN is the
N x 1 vector of unobserved residuals associated with the model specified in equation
(10).
The non-nested J test
While
the nested test requires the estimation of only one regression model, the non-nested,
J test requires estimating four regressions.
First, returning to null hypothesis in equation (8), the regression
model is estimated and the N x 1 vector of the predicted values of y, 
is obtained. Second, the regression model under the
alternative hypothesis in equation (9) is estimated and the N x 1 vector of
predicted values from this regression, 
, is also retrieved.
Third, the predicted values under the alternative hypothesis are added as another explanatory variable in the model specification under the null hypothesis and the following model is estimated:
The vector τ is a k x 1 vector of the regression parameters corresponding
to the intercept and the k – 1 explanatory variables that both the
specifications have in common. The regression
parameters 
and 
are 1 x 1 scalars with
denoting the slope
coefficient associated with the explanatory variable w in equation (11) and is the slope
coefficient corresponding to the predicted values from the model based on the
alternative hypothesis. As usual, e1 is the N x 1 residual
vector of white noise.
Fourth
and finally, predicted values found from estimating the model under the null hypothesis,
, are added as an additional explanatory variable to the
model specified under the alternative hypothesis. This requires estimating the regression
where κ is the k x 1 vector of unknown regression parameters
associated with the model’s intercept and the slope coefficients of the k -1
explanatory variables that are common in both models. The N x 1 vector of regression residuals is e2. Both 
and 
are unknown 1 x 1
scalars. The parameter is the unknown slope
coefficient associated with the vector w
and is the unknown slope
parameter associated with the predicted values obtained from estimating the
model under the null hypothesis, .
IV. WHEN THE NESTED AND NON-NESTED TESTS ARE EQUIVALENT
The two econometric models presented in the previous section of the paper are assumed to be identical except for one explanatory variable. Given this assumption, both the non-nested and the nested specification tests give equivalent results with the same test statistics, at least in absolute value. Three propositions about equations (10), (11) and (12) can be proven. These equations are replicated below for the reader’s convenience.
(10)
(11)
(12)
In the propositions that follow, the
following notation is used. Let 
denote the OLS
estimate for in equation (10). If se() is the standard error of , then the simple t test used to determine whether is statistically
different from zero has a test statistic equal to 
where
Similar
notation is used for 
, 
, 
, 
, and 
. The three
propositions are listed below.
Proposition #1: Given the assumptions of the null and
alternative hypotheses, then 
and 
. Thus, the nested and
non-nested specification tests yield the same test statistics in absolute
value.
Proposition #2: Given the assumptions of the null and
alternative hypotheses, 
, 
and 
. Likewise, 
, 
and 
. Thus, the
coefficients of the debated explanatory variables in both the non-nested and
the nested regression have the same estimates, standard errors, and t
statistics.
Proposition #3: Given the assumptions of the null and
alternative hypotheses, each observation of equations (10), (11) and (12) have
the same residual. In other words, 
. Thus, the non-nested
and nested specification tests have the same set of regression diagnostic
statistics.
The first proposition, the key result of the paper, is proven in the next section.[5] To prove the second proposition, mimic the steps and techniques used to prove the first proposition. The third proposition follows from the first two results.
V. PROVING PROPOSITION #1
The discussion that follows uses
simple matrix algebra to prove the first proposition. The key assumption is that two theoretically
plausible model specifications differ only by one explanatory variable. In this special case, the test statistic
derived by the non-nested J test and the test statistic derived by the nest
specification test have the same absolute value.
First: The Nested Specification in Equation (10)
To
prove Proposition #1, the formulas for the OLS estimates of and are derived, as are
formulas for the standard errors of these estimates. Given the formula of the estimates and
standard errors of these parameters, proving the first proposition rests on
demonstrating that the t statistics associated with each of the estimates have
the same absolute value.
The
strategy to prove these results will be mimicked at several steps. First, the OLS estimates for equations (10)
and (11) are derived by partitioning the matrices involved, taking the inverse
of these partitioned matrices, performing the necessary matrix multiplication,
and then simplifying the expressions.
Showing that the t statistics of two different equations have the same
absolute value also relies on the properties of idempotent and symmetric
matrices. Attention is first directed
towards the nested model specification test in equation (11).
The OLS estimate for 
, the coefficient of z
in equation (10)
Examining the regression with the nested hypothesis first, the data matrix and the vector of parameters can be partitioned so that
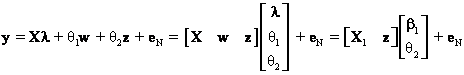
where X1 is a partitioned matrix and 
is a partitioned
vector so that
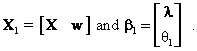
The OLS estimates of the intercept and slope coefficients are equal to
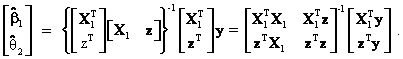
Using the well-known formula for the inverse of a partitioned matrix[6], the above equation can be simplified to obtain
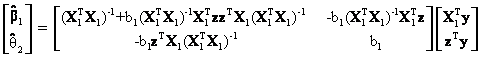
where b1 is a 1 x 1 scalar such that
Referring to equation (16), 
where I is the
identity matrix and M1 is
a symmetric, idempotent matrix. After
performing the matrix multiplication shown in equation (15) and simplifying, it
can be shown that the OLS estimate of equals
Since M1 is symmetric and idempotent, and equivalent expression for equation (17) is
The estimate for 
the variance of the
residuals in equation (10)
If
is the vector of
residuals obtained from estimating equation (10), then the variance of these residuals,
, is equal to
In this case, MN is the well-known and familiar idempotent and
symmetric matrix associated with the regression in equation (10) and
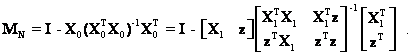
Again using the formula for the inverse of a partitioned matrix, MN in equation (20) can be written as
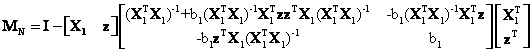
where b1 is still
defined as it was in equation (16) or 
. After performing the
indicated matrix multiplication in equation (21) and simplifying the results,
the relationship between MN
and M1 becomes
Therefore, equation (19) can be expanded and the OLS estimate of the variance of the errors terms in equation (10) becomes
or, using the fact that M1 is idempotent,
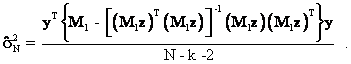
The standard error of 
or se()
To
construct the simple t statistic for , the standard error of is need. The variance of equals multiplied by b1
= (zTM1z)-1. This follows because b1 is the
element appearing in row k +2 and column k + 2 of the first matrix on the
right-hand side of the equal sign in equation (15).
Therefore,
the standard error of , denoted by se(), is equal to the square root of its variance or
Again, the last equality on the
right-hand side of equation (24) follows from the properties of idempotent
matrix M1.
Second: The Non-Nested J Test Specification in Equation (11)
The
next major step in proving Proposition #1 is deriving the formula for the OLS
estimate of in equation (11). In addition, formulas for the standard error
of and its corresponding
t statistic must also be derived. Just as equation (10) was partitioned in to
several submatrices, equation (11) can be written as
Recall from equation (14) that X1 is a partitioned matrix
where X1 = [X w] and similar to , 
is also a partitioned
vector in that
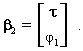
The vector of OLS estimates equals
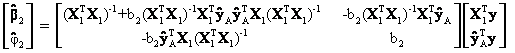
where 
and M1 is as defined before, 
.
Mimicking the steps performed on
equation (10), the OLS estimate for equals
The result for in equation (26) is
similar to the formula for in equation (18). If 
is the N x 1 vector of
residuals for equation (11), then it
follows from the previous derivations that the OLS estimate of the variance of
the random errors in equation (11) equals
Since M1 is symmetric and idempotent, this implies 
, 
, and equation (29) may be written as
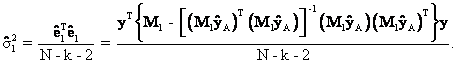
Like the standard error of discussed previously,
the standard error of , se(), equals
Digression:
The Properties of the Idempotent Matrix M1
To
show that 
, the properties of 
must be determined. Since X1
= [X w], then M1 is equal to
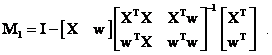
Using the formula for the inverse of a partitioned matrix, performing the matrix multiplication and simplifying the results gives the following expression
Referring to equation (33), M = I – X(XTX)-1XT and M is another idempotent, symmetric matrix. Also b3 is the bottom, right-hand term of the inverse of the partitioned matrix in equation (32) and b3 = (wTMw)-1.
Proving
Proposition #1 rests on showing the relationship between two vectors: 
and 
. and its transpose
appears frequently in the equations (18) and (24), the equations for and se(), while and its transpose are
seen in equations (28) and (31), the formulas for and se(). The product of M1
and z equals
Since 
, may be written as
= 
because M is idempotent and MX = [I – X(XTX)-1XT]X = X – X = 0.
The first key result to demonstrate: 
Equation
(35) gives the key resulted needed to prove Proposition #1. The first thing to demonstrate is that 
. This result is obtained through repeated
substitution starting with equation (30) and the steps are shown below.
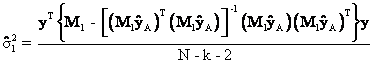
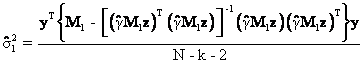
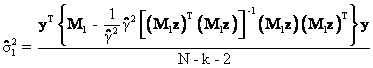
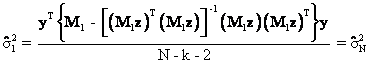
Equation (36) follows from the
equations directly above it because the transpose of the 1 x 1 scalar, 
, equals itself and the inverse of the 1 x 1 scalar 
is its reciprocal or 
.
Thus,
the OLS estimate of the variance of the residuals in equations (10) and (11) is
the same or . Let the OLS estimate
of the variance of the residuals in equation (12) equal 
. Since choice of the
null hypothesis and the alternative hypothesis is arbitrary (the original null
hypothesis can become the new alternative hypothesis while the initial
alternative hypothesis is now denoted as the new null hypothesis), variables
can be relabeled, and therefore 
.
The second key result to demonstrate: 
Given
that and = , it is now easy to show the relationship between se() and se(). From equation (31),
se() equals
or
.
Equation (37) follows from the
mathematical relationships used to obtain the results in equation (36). Therefore, 
and, as shown below, the
same mathematical relationships used above will be used to demonstrate a
similar relationship between and .
The third key result to demonstrate: 
The
formula for the OLS estimate of is in equation (28). Beginning with that equation, repeated
substitution and simplifying will show that 
. The steps of this
derivation follow.
Using previous key results to prove Proposition #1
Given
and , Proposition #1 can finally be proven. Proposition #1 states that if two competing
model specifications differ by only one explanatory variable, the test
statistic derived by the non-nested J test and the test statistic derived by
the nested, hybrid model have the same absolute value. This result follows from the linear
relationship between and and the linear
relationship between se() and se() because
.
Thus, in this special case where the two model specifications differ by one explanatory variable, both the non-nested J test and the nested, hybrid model give the same results.
V. CONCLUSION
Even though the J test involves running four regressions and the nested, hybrid model specification test only requires the estimation of two regressions, some argue that the J test is a superior test. There is increased probability that that multicollinearity will adverse effect the precision at which the parameters are estimated in the nested, hybrid model. The nested model may lack economic meaning and the results of the nested model may not be invariant to which specification is chosen as the reference model.
However, this paper shows that in the special case when two competing models differ by only one exogenous variable, the nested model specification test results in test statistics that have the same absolute value as the non-nested J test. In this case, obtaining statistical evidence on the correct model specification is quicker with the nested test than with the non-nested test. Estimation of one, and only one, nested, hybrid model results generates the same test statistics in absolute value that the non-nested J test generates after estimating four separate regressions. When two models differ by only one explanatory variable, use of the nested test offers some time savings in determining the correct model over using the non-nested J test.
REFERENCES
Breusch, T. S. “Testing for Autocorrelation in Dynamic Linear Models.” Australian Economic Papers, 17(31), 1978, 334 – 355.
Chow,
Gregory. “Tests of Equality Between Sets
of Coefficients in Two Linear Regressions.”
Econometrica, 28(3), July
1960, 591 – 605.
Davidson, R. and J. MacKinnon. “Several Tests for Model Specification in the Presence of Alternative Hypotheses.” Econometrica, 49(3), May 1981, 781-793.
Fomby,
T., R. Carter, and S. Johnson. Advanced Econometric Methods.
Godfrey,
L. G. “Testing Against General
Autoregressive and Moving Average Error Models When the Regressor include
Lagged Dependent Variable.” Econometrica, 46(6), November 1978, 1293 – 1302.
Gujarati,
D. Basic
Econometrics. 4th. ed.
Johnston,
J. and J. DiNardo. Econometric Methods. 4th.
ed.
Judge,
G.,
Kennedy,
P. A
Guide to Econometrics. 4th. ed.
Kmenta,
J. Elements
of Econometrics. 2nd. ed.
Maddala,
G. Introduction
to Econometrics.
McAleer, Michael. “The Significance of Testing Empirical Non-Nested Models.” Journal of Econometrics, 67(1), May 1995, 149-171.
Phillips,
A. W. “The Relationship Between
Unemployment and the Rate of Change of Money Wages in the
Thomas,
R. Modern
Econometrics: An Introduction.
Wooldridge,
J. Introductory
Econometrics: A Modern Approach. 2nd.
Ed.
. Obtain predicted values for Model A, 
, i = 1, …, N.
.
.
,
, the OLS estimate for 
, (the test statistic for the null hypothesis that 
.
, the t-statistic associated with 
, the OLS estimate for 
, (the test statistic for the null hypothesis that 
.
.
, and obtain the R2 associated with this nested or
hybrid regression, 
.
, while the alternative hypotheses is HA: Not
all the 
.