CSSE 230
Data Structures and Algorithm Analysis
Written Assignment 7
- 78 points
To Be Turned In
Submit to the WA7 drop box on ANGEL. Late days may be used for written assignments.
-
Don’t forget: You should be keeping an individual log about your team project work so that you can write a performance evaluation for each of your teammates. You do not need to turn in this log, but I wanted to remind you while I had your attention.
-
(20 points) Consider the following directed graph:
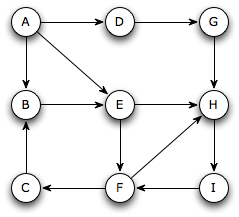
-
(5) Show the first three rows of an adjacency matrix for this graph. Label the rows and columns.
-
(5) Show an adjacency list representation of this graph.
-
(5) Show an edge list representation of this graph.
-
(5) Which of the above representation will use the least space? Support your answer with calculations. Be explicit about your assumptions concerning details of the representations.
- (15 points) Prove by mathematical induction that n! ≥ 2n for all integers n≥4.
(It can be proven other ways, but this is a good example for practicing induction, so that is what you should do).
-
(15 points) Weiss exercise 20.5 [20.5]. In this problem you will check your understanding of
collision resolution techniques in hash tables.
-
(12 points) Weiss Exercise 21.3[21.3]. The add and buildHeap algorithms are on pages 815 [753] and 819[757],
respectively. Do this one carefully.
It will be hard to know how to give partial credit for incorrect answers.
- ( 6 points) Weiss Exercise 8.10 [8.10]. Logarithmic form
of Stirling's approximation.
- (10 points) Weiss Exercise 21.8[21.8]. You should provide explanations for your formulas.
Notes: Suppose we decide to use the same "pointerless"
representation that we used for complete trees to represent ANY
tree by an array (for example, to find the parent of a node in
a[i], we look in a[i/2]). If
the tree is not complete, there will be some "gaps" in the
array, so extra space must be used. If the n-element tree
is complete, the size of the array is n+1. The question is
asking how large the array must be if the n elements are
arranged into various trees of different shapes. For each part,
you should give the answer for the worst case, i.e. when the
nodes at the extra levels are as far right in the tree as they
can be. Answers to the questions should be formulas (functions
of n).
Optional practice problem
- not to be turned in.
This problem has been assigned in the past. Since you are actually implementing height-balanced trees, it seems redundant. But it could still be a very good practice problem for the next exam, so I did not remove it.
(xx points) Start with the following Binary Search Tree:
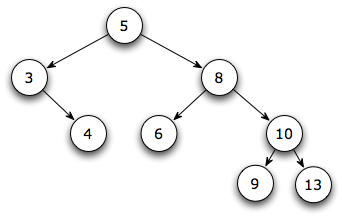
See the hint at the end!
-
Is this an AVL tree? ____ If not, rearrange it so that it is height-balanced.
-
Draw the tree after insertion of a node containing 11, using the usual BST insertion algorithm.
-
Is the new tree AVL? ______ If not, name the node where the rotation should be done, according to the algorithm from class. ______ Single or double rotation? ____________ If you need to do a rotation, draw the resulting tree.
-
Delete the element 5 from the original tree (not the one from part c), using the BST deletion algorithm described in class and in the textbook. Draw the new tree.
-
Is the new tree AVL? ______ If not, name the node where the rotation should be done, according to the algorithm from class. ______ Single or double rotation? ____________ If you need to do a rotation, draw the resulting tree.
-
Is your new tree (if any) AVL? ______ If not, name the node where the rotation should be done, according to the algorithm from class. ______ Single or double rotation? ____________ If you need to do a rotation, draw the resulting tree.
-
Add the element 5 to the tree from part (f) using the BST algorithm. Draw the new tree.
-
Is the new tree AVL? ______ If not, name the node where the rotation should be done, according to the algorithm from class. ______ Single or double rotation? ____________ If you need to do a rotation, draw the resulting tree.
-
Add the element 12 to the tree from part (h). Draw the new tree.
-
Is the new tree AVL? ______ If not, name the node where the rotation should be done, according to the algorithm from class. ______ Single or double rotation? ____________ If you need to do a rotation, draw the resulting tree.
-
Add the element 7 to the tree from part (j). Draw the new tree.
-
Is the new tree AVL? ______ If not, name the node where the rotation should be done, according to the algorithm from class. ______ Single or double rotation? ____________ If you need to do a rotation, draw the resulting tree.
Hint: In my solution, for all the sub-parts together, I did three single rotations and no double rotations. The first four leaf nodes in my final tree were 3, 5, 7, and 9. (In my first attempt, I misread part d) and deleted from the tree in part c) rather than the original tree. With that mistake, for all the sub-parts together, I did two single rotations and one double rotation and the first four leaf nodes in my final tree were also 3, 5, 7, and 9.)

